library(sf, quietly = TRUE)
library(ggplot2, quietly = TRUE)
library(tmap, quietly = TRUE)
library(dplyr, quietly = TRUE)
library(ggpubr, quietly = TRUE)
library(mgcv, quietly = TRUE)
library(spdep, quietly = TRUE)
library(collapse, quietly = TRUE)
library(gratia, quietly = TRUE)
# Chargement des données
data_airbnb <- readRDS('data/airbnb.rds')
data_airbnb$super_hote <- ifelse(data_airbnb$host_is_superhost == 't', 'YES', 'NO')
data_airbnb$prive <- factor(data_airbnb$private, levels = c('Chambre', 'Entier'))
data_airbnb$stationnement_gratuit <- factor(data_airbnb$Free_street_parking, levels = c('NO', 'YES'))
data_airbnb$jardin_ou_cours <- factor(data_airbnb$Garden_or_backyard, levels = c('NO', 'YES'))
data_airbnb$super_hote <- factor(data_airbnb$super_hote, levels = c('NO', 'YES'))
data_airbnb$metro_500m <- factor(data_airbnb$has_metro_500m, levels = c('NO', 'YES'))
# Nous regarderons l'impact de 10 évaluations supplémentaires
data_airbnb$number_of_reviews <- data_airbnb$number_of_reviews / 10
model_data <- data_airbnb %>%
dplyr::select(any_of(c('price','private','stationnement_gratuit', 'jardin_ou_cours',
'bedrooms', 'super_hote',
'number_of_reviews','review_scores_rating','metro_500m',
'prt_veg_500m'))) %>%
filter(complete.cases(st_drop_geometry(.)))
model_data$log_price <- log(model_data$price)
XY <- st_coordinates(model_data)
model_data$X <- XY[,1]
model_data$Y <- XY[,2]
# Modèle non spatial
model1 <- gam(log_price ~ private + bedrooms +
stationnement_gratuit + jardin_ou_cours +
number_of_reviews + review_scores_rating + super_hote +
prt_veg_500m + metro_500m,
data = model_data, method = 'REML',
family = scat)
# Modèle intégrant uniquement la constante variant spatialement
model2 <- gam(log_price ~ private + bedrooms +
stationnement_gratuit + jardin_ou_cours +
number_of_reviews + review_scores_rating + super_hote +
prt_veg_500m + metro_500m +
s(X,Y, bs = 'gp'),
data = model_data, method = 'REML',
family = scat)10 Modèles GAM et GLMM avec des coefficients variant spatialement (en cours de révision)
Objectifs d’apprentissage visés dans ce chapitre
À la fin de ce chapitre, vous devriez être en mesure de :
- comprendre comment les modèles GAM et GLMM peuvent être adaptés pour explorer l’hétérogénéité spatiale;
- utiliser une spline pour une variable indépendante dans un modèle GAM;
- comprendre la notion de concurvité pour un modèle GAM;
- Introduire un effet aléatoire spatial pour une variable indépendante dans un modèle linéaire généralisé à effets mixtes (GLMM);
- mettre en pratique ces modèles spatiaux dans R.
Liste des packages utilisés dans ce chapitre
- Pour manipuler des données :
dplyretmatrixStatspour structurer et explorer des données.
- Pour importer et manipuler des fichiers géographiques :
sfpour importer et manipuler des données vectorielles.terrapour importer et manipuler des données raster.
- Pour cartographier des données :
ggplot2etggpubrpour construire des graphiques.tmappour construire des cartes thématiques.
- Pour construire des modèles spatiaux :
spdeppour construire des matrices de pondération spatiales et calculer le I de Moran.mgcv,gratiaetcollapsepour construire des modèles GAM.sdmTMBpour construire des modèles GLMM spatiaux.caretDHARMapour réaliser des diagnostics sur des résidus de modèles.
Dans les deux chapitres précédents, nous avons présenté la GWR et ses différentes extensions qui permettent d’explorer comment les relations entre la variable dépendante et les variables indépendantes d’un modèle de régression varient localement. Contrairement aux autres modèles abordés jusqu’ici, la GWR permet de répondre au problème de l’hétérogénéité spatiale plutôt que celui de la dépendance spatiale (section 1.6.2). Cependant, la GWR fait l’objet des multiples critiques décrites précédemment (section 8.4). En effet, bien qu’elle constitue une technique puissante d’exploration de données, elle comprend plusieurs limites d’ordre statistique qui restreignent fortement son utilisation dans le cadre d’analyses inférentielles.
Avec le développement de logiciels et de packages permettant de construire des modèles complexes, notamment les modèles à effets mixtes, de nouvelles approches ont été proposées pour intégrer la question de l’hétérogénéité spatiale dans les modèles. Nous verrons ici comment les modèles GAM et GLMM peuvent être utilisés pour faire varier spatialement les coefficients de régression, tout en évitant les limites propres à la GWR. Ces modèles peuvent être regroupés sous le terme de modèles à coefficients variant spatialement (spatially varying coefficients models ou SVCM).
Les modèles SVCM offrent deux avantages principaux comparativement aux modèles GWR. D’une part, ils permettent de capturer directement l’hétérogénéité spatiale dans un seul modèle tandis que la GWR produit une équation de régression pour chaque entité spatiale (section 8.1.2). D’autre part, les modèles SVCM ne nécessitent pas de spécifier une zone d’influence (bandwidth). De la sorte, les conditions d’application des modèles de régression sont ainsi (plus) faciles à satisfaire.
10.1 Hétérogénéité spatiale et modèles généralisés additifs (GAM)
Dans cette section, nous expliquons comment les splines que nous avions utilisées pour intégrer l’espace dans un modèle GAM (section 6.4) peuvent être utilisées pour faire varier spatialement l’effet de certains coefficients.
10.1.1 Splines et coefficients variant spatialement
Dans le chapitre 6, nous avons décrit les modèles GAM qui permettent de prendre en compte l’espace dans un modèle en intégrant une fonction non linéaire appelée spline. Cette fonction non linéaire capture l’effet des coordonnées spatiales (spline bivariée) ou de la matrice de voisinage (Markov Random Field). Nous avons que la complexité de cette fonction dépend du nombre de nœuds (k) qui lui est accordé et d’un paramètre de lissage déterminé le plus souvent comme une pénalisation similaire à un effet aléatoire. Ces splines spatiales capturent ainsi des structures spatiales lisses et caractérisées par une importante autocorrélation spatiale. À titre de rappel, un modèle GAM intégrant uniquement une spline spatiale est formulé de la façon suivante :
\[ \begin{aligned} &y \sim D(\mu,\theta)\\ &g(\mu) = \beta_0 + \beta X + f(sp)\\ \end{aligned} \tag{10.1}\]
avec :
- \(y\), la variable dépendante.
- \(D\), une distribution avec une espérance \(\mu\) et ses autres paramètres \(\theta\).
- \(X\), les variables indépendantes dont l’effet est supposé linéaire par le modèle.
- \(\beta\), les coefficients des variables indépendantes.
- \(\beta_0\), la constante.
- \(f\), une fonction modélisant l’impact de l’espace.
- \(sp\), une matrice de coordonnées cartésiennes ou une matrice de contiguïté spatiale.
La spline \(f(sp)\) permet d’augmenter ou de réduire spatialement la valeur prédite pour l’espérance de \(y\). Elle peut être vue comme une forme de bonus ou de malus local accordée à la constante. Pour étendre cet usage au cas des coefficients de régression variant spatialement, il est possible de construire une spline similaire, mais qui est multipliée par la variable indépendante dont le coefficient doit varier spatialement. Cette formulation suppose donc que la variation spatiale du coefficient doit suivre une tendance lisse. Le modèle peut donc être modifié de la façon suivante :
\[ \begin{aligned} &y \sim D(\mu,\theta)\\ &g(\mu) = \beta_0 + \beta X + \sum^{n}_{j=1}(f_j(sp)\times\zeta_j) + f(sp)\\ \end{aligned} \tag{10.2}\]
avec \(\zeta_j\), une variable indépendante variant spatialement.
Ce modèle permet de choisir quelles variables dépendantes doivent avoir des effets variant dans l’espace. Notez toutefois que chaque spline ajoutée augmente considérablement la complexité du modèle, c’est-à-dire le nombre de paramètres à estimer. Par conséquent, il est recommandé de choisir ces variables pour répondre à une question de recherche particulière ou encore à un élément du votre cadre théorique. Bien entendu, il est possible de comparer l’ajustement de plusieurs modèles imbriqués pour vérifier si l’ajout d’un coefficient variant spatialement complexifie le modèle de façon justifiée; autrement dit, si son apport est significatif. Pour ce faire, on peut comparer les valeurs d’AIC des différents modèles ou d’un test de rapport de vraisemblance. Notez que le test de rapport de vraisemblance basé sur la distribution du \(\chi^2\) n’est pas très adapté à ce type de modèle. Une alternative est la version non paramétrique par boostrap qui est toutefois très coûteuse en temps de calcul.
Enjeux de concurvité
Il n’est pas obligatoire de conserver la première spline faisant varier la constante du modèle. Cette dernière peut devenir inutile, une fois que certains coefficients de régression ont été autorisés à varier spatialement. Par ailleurs, il est possible que les différentes splines spatiales d’un modèle se superposent et génèrent alors un problème de concurvité.
La concurvité est l’équivalent de la multicolinéarité, mais pour les fonctions lisses estimées par les splines. Si deux termes non linéaires ont une forte concurvité, cela signifie que l’un des deux termes peut englober l’autre. Ce problème est fréquent dans un modèle où plusieurs coefficients varient spatialement avec des splines.
Bien que n’importe quel type de spline peut être utilisé, les gaussian process (bs = 'gp') sont généralement privilégiés, car ils sont utilisés dans d’autres modèles spatiaux, notamment les GLMM. En effet, rappelons brièvement qu’une spline est mathématiquement équivalente à un effet aléatoire (Wood 2017). Dit plus simplement, les GAM sont en réalité des GLMM. Il est important ici de distinguer deux tests de significativité à effectuer sur les splines d’un modèle GAM :
Le premier test (typiquement obtenu avec la fonction
summarydemgcv) permet de déterminer si l’effet général de la spline est différent de zéro. D’un point de vue pratique, il est comparable au test appliqué aux coefficients classiques d’un modèle linéaire permettant de déterminer s’ils sont ou non significativement différents de zéro.Le second test consiste à vérifier si les différentes valeurs de la spline sont significativement différentes de zéro. En effet, une spline utilisée pour obtenir des coefficients variant spatialement peut produire des coefficients qui ne sont pas significativement différents de zéro partout. Ce deuxième test est généralement réalisé avec une approche par simulation, mais peut aussi être réalisé avec une approche par bootstrap. Cette deuxième approche est plus exacte, mais nécessite un temps de calcul beaucoup plus élevé. D’un point de vue pratique, ce test permet de déterminer où sur notre territoire notre variable indépendante est associée avec un coefficient significativement différent de zéro. Il est important d’effectuer ce test pour ne pas surinterpréter les résultats du modèle.
10.1.2 Mise en œuvre dans R
Nous illustrons ici l’utilisation des splines pour faire varier spatialement les coefficients d’un modèle, avec l’exemple donné dans le chapitre 2 sur les GLS. Pour rappel, nous modélisons le logarithme du prix par nuit de logements Airbnb sur l’île de Montréal. Nous commençons par réajuster le modèle non spatial (model1) et le modèle GAM simple (model2). Puis, nous tenterons d’améliorer le modèle en faisant varier spatialement certains coefficients (model3).
Pour le troisième modèle (model3), nous autorisons plusieurs coefficients à varier spatialement :
- le fait qu’un logement soit privé;
- la présence d’une station de métro à moins de 500 mètres;
- la densité de la couverture végétale dans un rayon de 500 mètres.
Notez que nous avons retiré la constante variant spatialement (s(X,Y, bs = 'gp')). En effet, après plusieurs tests, il s’est avéré que cet effet spatial était capable de résumer à lui seul les effets des coefficients variant spatialement (phénomène de concurvité). Nous comparons donc le modèle 2 avec cette constante spatiale et le modèle 3 privilégiant des coefficients variant spatialement.
# Pour les variables dichotomiques, il est plus facile de les recoder comme
# des variables binaires pour ce type de modèle
model_data$private <- ifelse(
model_data$private == 'Entier', 1, 0
)
model_data$metro_500m <- ifelse(
model_data$metro_500m == 'YES', 1, 0
)
model_data$jardin_ou_cours <- ifelse(
model_data$jardin_ou_cours == 'YES', 1, 0
)
model_data$stationnement_gratuit <- ifelse(
model_data$stationnement_gratuit == 'YES', 1, 0
)
model_data$super_hote <- ifelse(
model_data$super_hote == 'YES', 1, 0
)
model3 <- gam(log_price ~ bedrooms +
stationnement_gratuit + jardin_ou_cours +
number_of_reviews + review_scores_rating + super_hote +
s(X,Y, bs = 'gp', k = 25, by = private) +
s(X,Y, bs = 'gp', k = 25, by = metro_500m) +
s(X,Y, bs = 'gp', k = 25, by = prt_veg_500m),
data = model_data, method = 'REML',
family = scat)
round(concurvity(model3),3) para s(X,Y):private s(X,Y):metro_500m s(X,Y):prt_veg_500m
worst 0.997 0.978 0.811 0.978
observed 0.997 0.739 0.677 0.800
estimate 0.997 0.619 0.559 0.516Les valeurs de concurvité ci-dessus indiquent pour chaque terme du modèle s’il peut être inclus dans un autre terme non linéaire. Il s’agit d’une extension de la notion de multicolinéarité aux termes non linéaires. Les valeurs sont comprises entre 0 (absence de concurvité) et 1 (concurvité parfaite). Le terme para indique la partie paramétrique du modèle (les effets linéaires). Trois estimations de la concurvité sont fournies : pessimistes (worst), optimistes (observed) et équilibrées (estimate). Dans notre cas, les valeurs de la ligne estimate pour les termes non linéaires sont toutes relativement faibles, indiquant que ces derniers ne peuvent pas se substituer les uns aux autres. Notez ici que le package mgcv utilise une méthode d’estimation robuste qui est peu affectée par une concurvité modérée. Cependant, des valeurs supérieures à 0,8 devraient être considérées comme problématiques.
Nous comparons les trois modèles en nous basant sur trois mesures : l’AIC, le REML et le R2 qui signalent que le modèle 2 semble être le plus intéressant (moins de paramètres, plus faibles valeurs pour l’AIC et le REML, valeur de R2 la plus élevée; tableau 10.1). Toutefois, ce modèle fournit peu d’informations sur les variations spatiales des facteurs explicatifs du prix des Airbnb. Il est donc pertinent d’analyser en détail le troisième modèle.
comp_df <- AIC(model1, model2, model3)
comp_df$REML <- c(model1$gcv.ubre, model2$gcv.ubre, model3$gcv.ubre)
comp_df$R2 <- c(summary(model1)$r.sq,
summary(model2)$r.sq,
summary(model3)$r.sq)
knitr::kable(comp_df,
row.names = TRUE,
digits = 2,
format.args = list(decimal.mark = ',', big.mark = " "),
)| df | AIC | REML | R2 | |
|---|---|---|---|---|
| model1 | 12,00 | 2 732,44 | 1 392,92 | 0,44 |
| model2 | 31,63 | 2 610,63 | 1 365,34 | 0,47 |
| model3 | 41,33 | 2 638,35 | 1 422,61 | 0,46 |
Bien entendu, nous vérifions préalablement si ce troisième modèle respecte les différentes conditions d’application en examinant notamment l’autocorrélation spatiale de ses résidus.
model_data$residual_3 <- residuals(model3, type = 'scaled.pearson')
model_data$residual_2 <- residuals(model2, type = 'scaled.pearson')
model_data$residual_1 <- residuals(model1, type = 'scaled.pearson')
knn_list <- knearneigh(model_data, k = 10)
nb_list <- knn2nb(knn_list, sym = TRUE)
listw <- nb2listwdist(nb_list, model_data , style = 'W', type = 'idw', alpha = 2)
test3 <- moran.mc(model_data$residual_3, listw = listw, nsim = 999)
test2 <- moran.mc(model_data$residual_2, listw = listw, nsim = 999)
test1 <- moran.mc(model_data$residual_1, listw = listw, nsim = 999)
test0 <- moran.mc(model_data$log_price, listw = listw, nsim = 999)
tableau <- data.frame(
variable = c('residus3', 'residus2', 'residus1', 'log_price'),
I = c(test3$statistic, test2$statistic, test1$statistic, test0$statistic),
P = c(test3$p.value, test2$p.value, test1$p.value, test0$p.value)
)
tableau variable I P
1 residus3 0.07124715 0.001
2 residus2 0.06724634 0.001
3 residus1 0.12514665 0.001
4 log_price 0.11013959 0.001Le test du I de Moran sur les résidus n’indique pas de présence d’autocorrélation spatiale pour le modèle 3. Affichons maintenant les résultats du modèle avec la fonction summary.
summary(model3)
Family: Scaled t(10.425,0.389)
Link function: identity
Formula:
log_price ~ bedrooms + stationnement_gratuit + jardin_ou_cours +
number_of_reviews + review_scores_rating + super_hote + s(X,
Y, bs = "gp", k = 25, by = private) + s(X, Y, bs = "gp",
k = 25, by = metro_500m) + s(X, Y, bs = "gp", k = 25, by = prt_veg_500m)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.813430 0.168467 16.700 < 2e-16 ***
bedrooms 0.239156 0.011080 21.585 < 2e-16 ***
stationnement_gratuit 0.044686 0.019975 2.237 0.0253 *
jardin_ou_cours -0.018990 0.027892 -0.681 0.4960
number_of_reviews 0.001394 0.001924 0.724 0.4688
review_scores_rating 0.007420 0.001711 4.337 1.45e-05 ***
super_hote 0.036737 0.021893 1.678 0.0933 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(X,Y):private 6.415 8.073 995.14 < 2e-16 ***
s(X,Y):metro_500m 9.422 11.306 23.05 0.02175 *
s(X,Y):prt_veg_500m 11.939 14.677 36.27 0.00143 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.461 Deviance explained = 45.3%
-REML = 1422.6 Scale est. = 1 n = 2260Nous constatons que les trois splines ont des effets significativement différents de 0 (premier test; voir la section Approximate significance of smooth terms). Par conséquent, nous utilisons la méthode des effets marginaux pour représenter leurs coefficients dans l’espace et valider leur significativité localement (second test). Le package mgcv facilite l’extraction de ces effets grâce à la fonction predict avec le paramètre type = 'terms', qui va garder séparément les contributions des différentes composantes du modèle.
Puisque nous modélisons le logarithme du prix des logements, il convient de transformer les coefficients avec la fonction exponentielle pour les interpréter dans l’échelle originale ($); leurs effets sont ainsi multiplicatifs plutôt qu’additifs.
library(terra)
library(gratia)
library(matrixStats)
# Création d'un masque pour ne représenter l'effet des splines que dans les
# secteurs dans lesquels nous avons des données
mask_data <- st_read('data/chap10/ILE_MTL.shp', quiet = TRUE) %>%
st_transform(st_crs(data_airbnb)) %>%
st_intersection(st_buffer(data_airbnb, 1500)) %>%
st_union() %>%
vect()
# Préparation d'un ensemble de points de prédictions formant une grille
# régulière de quadrats de 200 mètres de coté
bbox <- as.list(st_bbox(st_buffer(data_airbnb,1000)))
coords <- expand.grid(
X = seq(bbox$xmin, bbox$xmax, 200),
Y = seq(bbox$ymin, bbox$ymax, 200)
)
# Création du dataframe pour les prédictions
pred_df <- coords
pred_df$private <- 1
pred_df$bedrooms <- 0
pred_df$stationnement_gratuit <- 0
pred_df$jardin_ou_cours <- 0
pred_df$number_of_reviews <- 0
pred_df$review_scores_rating <- 0
pred_df$super_hote <- 0
pred_df$prt_veg_500m <- 25
pred_df$metro_500m <- 1
# Prédictions à partir du modèle
preds <- predict(model3, newdata = pred_df, type = 'terms')
preds <- data.frame(preds)
pred_df <- cbind(pred_df, preds)
# Conversion des coefficients en exponentielle pour avoir les effets sur
# l'échelle originale des données ($)
pred_df$coeff_private <- exp(pred_df$s.X.Y..private)
pred_df$coeff_prt_veg_500m <- exp(pred_df$s.X.Y..prt_veg_500m)
pred_df$coeff_metro_500m <- exp(pred_df$s.X.Y..metro_500m)
# Conversion des prédictions en objets raster pour la cartographie
vars <- c(c("X", "Y","coeff_private", "coeff_prt_veg_500m","coeff_metro_500m"))
data_rast <- as.matrix(pred_df[, vars])
raster_private <- rast(data_rast[,c(1,2,3)],type = 'xyz')
crs(raster_private) <- crs(data_airbnb)
raster_veg <- rast(data_rast[,c(1,2,4)],type = 'xyz')
crs(raster_veg) <- crs(data_airbnb)
raster_metro <- rast(data_rast[,c(1,2,5)],type = 'xyz')
crs(raster_metro) <- crs(data_airbnb)
# Chargement des lignes de métro pour la cartographie
metro <- st_read('data/chap10/stm_lignes_sig.shp',quiet = TRUE) %>%
st_transform(st_crs(data_airbnb)) %>%
filter(grepl('Ligne',route_name, fixed = T)) %>%
mutate(route_name = gsub(".*- ", "", route_name))
metro_colors <- c('Verte' = '#008E4F',
'Orange' = '#EF8122',
'Jaune' = '#FFE300',
'Bleue' = '#0083C9'
)
# Cartographie des trois rasters
legende_parametres <- list(text.separator = "à",
decimal.mark = ",",
big.mark = " "
)
tmap_options(frame = FALSE)
tm_shape(mask(raster_private, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(1, 1.15, 1.30, 1.50, 1.70, 1.80, 1.9, 2.05),
midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
col.legend = tm_legend(title = "Coefficient logement privé (exp)",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top"))
) +
tm_shape(data_airbnb) + tm_dots(size = .1)
tm_shape(mask(raster_veg, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0.8, 0.9, 0.95, 1, 1.05, 1.1, 1.2),
midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
col.legend = tm_legend(title = "Coefficient couverture végétale (exp)",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top"),
)
) +
tm_shape(data_airbnb) +
tm_dots(size = .1)
tm_shape(mask(raster_metro, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0.7, 0.8, 0.9, 1, 1.15, 1.30, 1.5, 2, 6),
values = '-brewer.rd_bu',
midpoint = 1,
label.format = legende_parametres),
col.legend = tm_legend(title = "Coefficient métro à 500 m (exp)",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top")
)
) +
tm_shape(data_airbnb) +
tm_dots(size = .1) +
tm_shape(metro) +
tm_lines(col = 'route_name',
lwd = 4,
col.scale = tm_scale_categorical(values = metro_colors),
col.legend = tm_legend(title = "Ligne de métro",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top"),
)
) +
tm_shape(data_airbnb) + tm_dots(size = .1)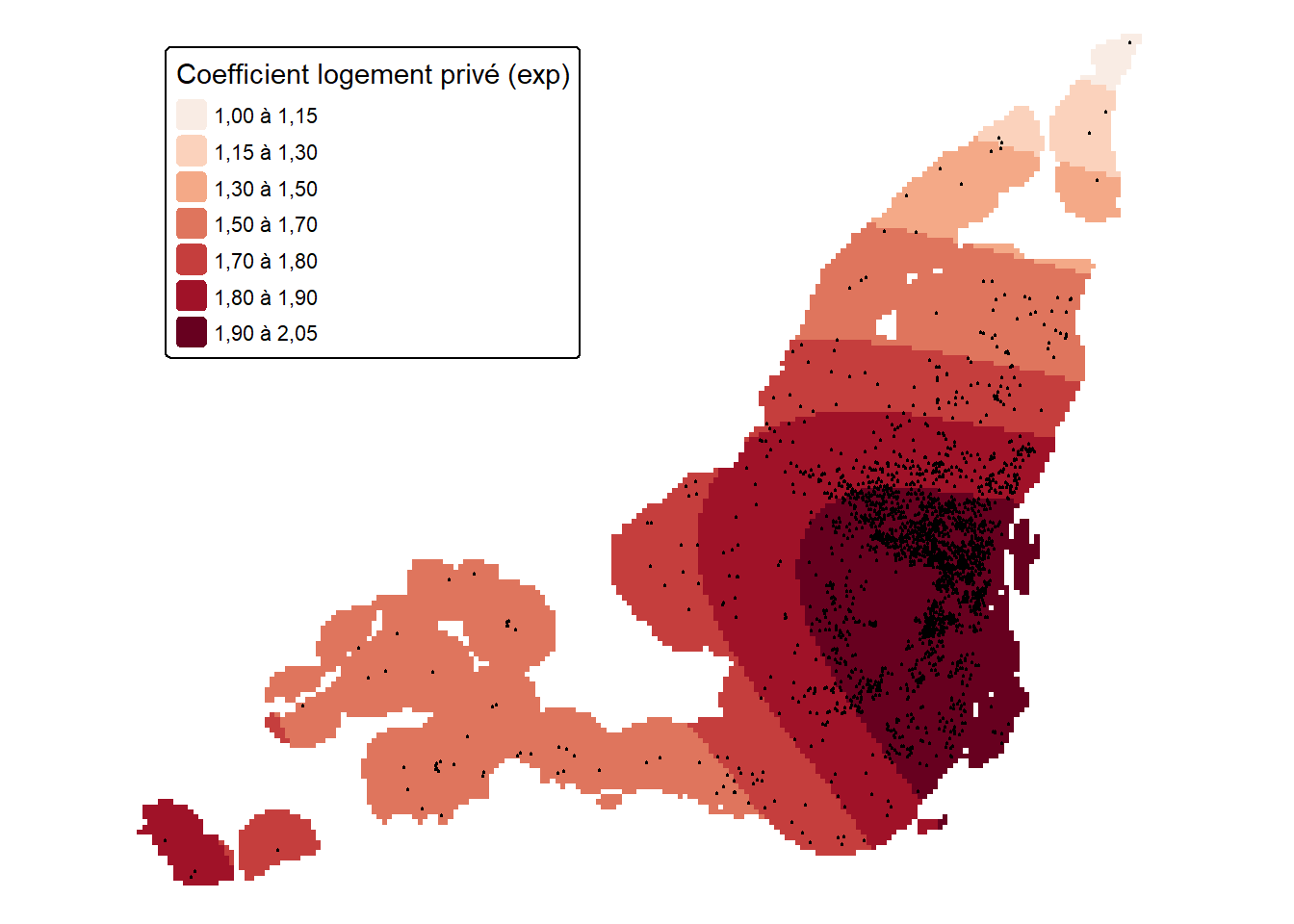
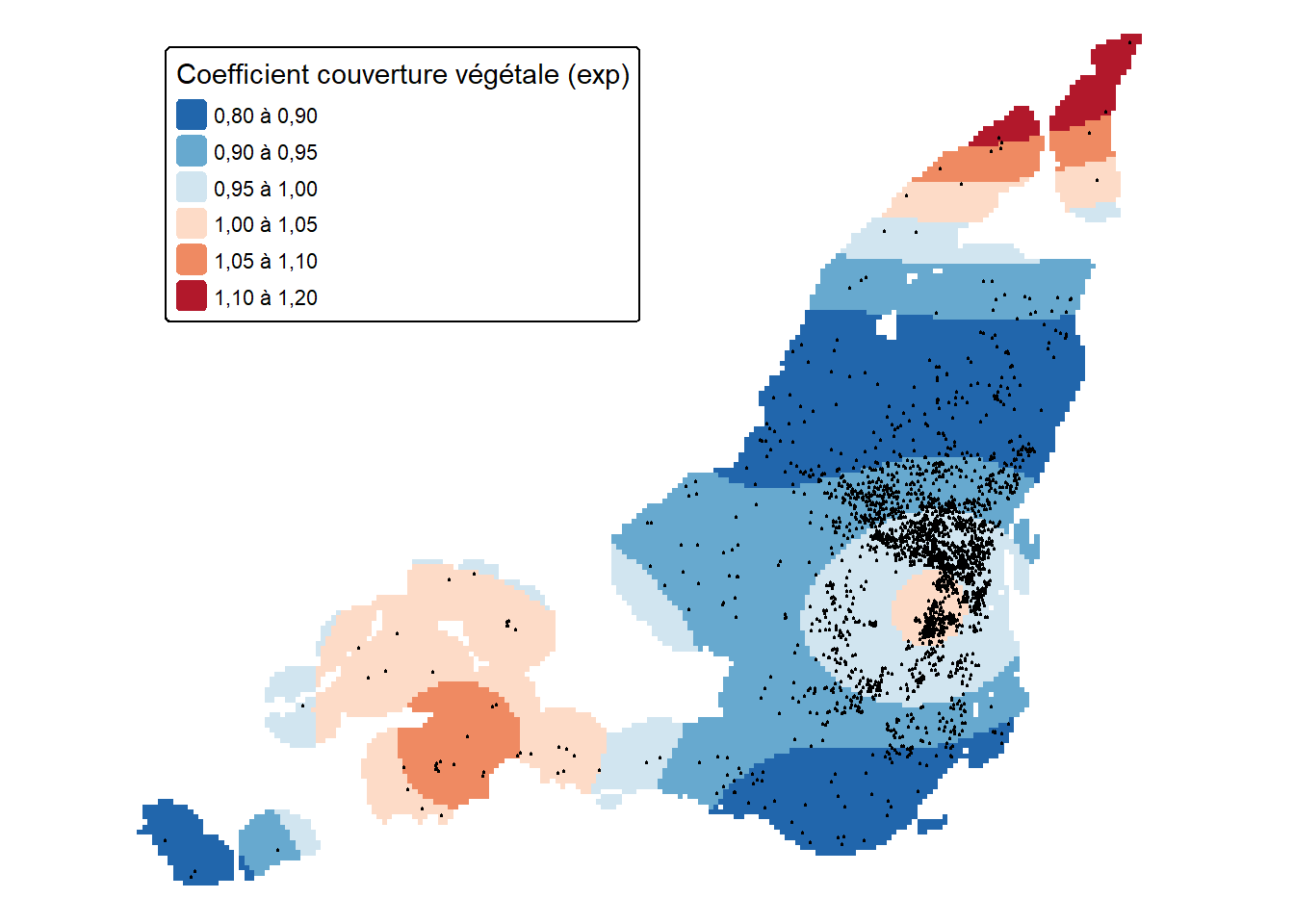
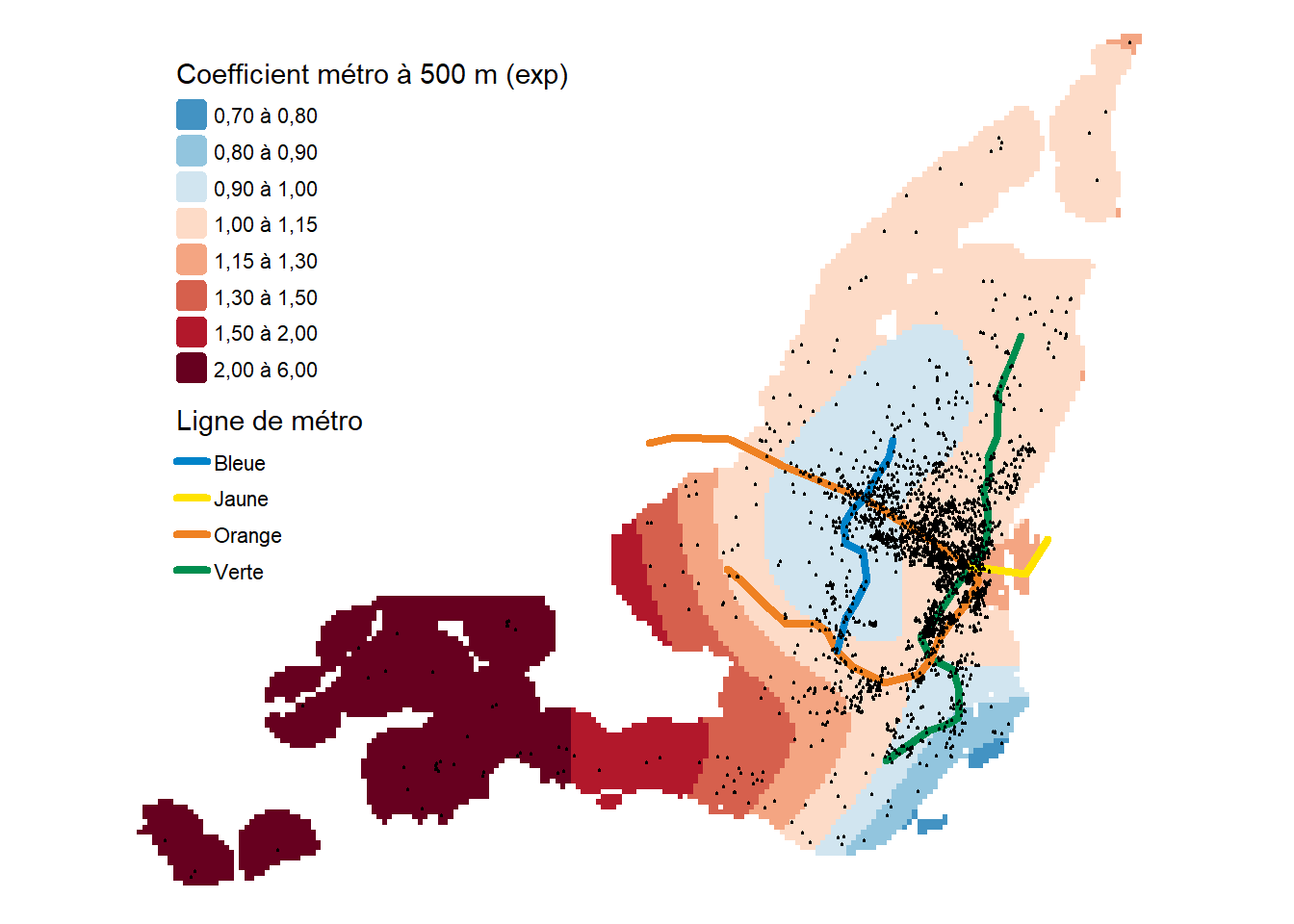
Les figures 10.1 à 10.3 illustrent les trois splines ajustées à nos coefficients variant spatialement.
Pour le métro (figure 10.3), il est important de ne pas interpréter les valeurs en dehors de la zone dans laquelle nous avons des stations de métro. En effet, les splines ont tendance à mal interpoler les valeurs en dehors de l’étendue observée, car elles se contentent de prolonger la tendance. Nous observons que les prix des logements Airbnb tendent à être plus faibles le long de la ligne bleue, mais aussi le long de la portion Ouest de la ligne verte. Il s’agit d’une réduction relativement faible (< 10 %). À proximité de la station Berry-UQAM, permettant la connexion entre les lignes orange, jaune et verte, nous pouvons observer des prix des Airbnb légèrement plus élevés de 15 % à 30 % pour les Airbnb à moins de 500 mètres d’une ligne de métro.
Une augmentation de 25 points de pourcentage de la densité végétale est associée avec des réductions de prix pouvant allant jusqu’à 20 % (figure 10.2). Ces réductions suivent généralement un gradient concentrique autour du centre-ville. Proche du Mont-Royal, l’impact de la densité végétal est légèrement positif avec une augmentation des prix atteignant 5 %. Dans l’Ouest, dans l’arrondissement Pointe-Claire, l’impact du couvert végétal semble plus élevé encore (de 5 à 10 %). Cependant, nous disposons d’assez peu d’observations pour confirmer cette observation.
Le fait que le logement soit privé a toujours un impact positif le prix du logement. Cependant, cet effet est bien supérieur au Centre-Ville et dans les quartiers centraux dans lesquels le prix des Airbnb est au moins doublé. Plus on s’éloigne du Centre-Ville, plus l’effet diminue, atteignant par exemple une augmentation de seulement 50 % au niveau de l’arrondissement Montréal-Est.
Attention, cette interprétation repose uniquement sur les valeurs moyennes prédites pour les coefficients variant spatialement. Si la valeur de p d’une spline est significative pour le modèle général (premier test), cela ne veut pas dire que sa contribution est significativement différente de zéro sur l’ensemble de son domaine de définition (second test).
Nous calculons donc ci-dessous des pseudovaleurs de p locales pour déterminer si les coefficients locaux sont significativement différents de zéro. Pour ce faire, nous utilisons deux approches. La première est basée sur une approximation via une distribution normale. Elle est considérée valide lorsque le nombre d’observations est grand.
# Extraction des termes et de leur écart-type
preds <- predict(model3, newdata = pred_df, type = 'terms', se = T )
fit <- data.frame(preds$fit)
se <- data.frame(preds$se.fit)
terms <- c('prt_veg_500m', 'private', 'metro_500m')
for(term in terms){
sterm <- paste0('s.X.Y..', term)
z <- (fit[[sterm]] / se[[sterm]])
pval <- 2 * (1 - pnorm(abs(z)))
pred_df[[paste0('sign_',term)]] <- pval
}
# Conversion des prédictions en objets raster pour la cartographie
vars <- c(c("X", "Y","sign_private", "sign_metro_500m","sign_prt_veg_500m"))
data_rast <- as.matrix(pred_df[, vars])
raster_private <- rast(data_rast[,c(1,2,3)],type = 'xyz')
crs(raster_private) <- crs(data_airbnb)
raster_veg <- rast(data_rast[,c(1,2,5)],type = 'xyz')
crs(raster_veg) <- crs(data_airbnb)
raster_metro <- rast(data_rast[,c(1,2,4)],type = 'xyz')
crs(raster_metro) <- crs(data_airbnb)
colors <- rev(c('#F7F7F7','#D1E5F0', '#92C5DE', '#4393C3', '#2166AC'))
tm_shape(mask(raster_private, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0, 0.05, 0.1, 0.2, 0.3, 1),
values = colors,
label.format = legende_parametres),
col.legend = tm_legend(title = "Valeur de p (norm.) pour le \ncoefficient logement privé",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top")
)
) +
tm_shape(data_airbnb) +
tm_dots(size = .1)
tm_shape(mask(raster_veg, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0, 0.05, 0.1, 0.2, 0.3, 1),
values = colors,
label.format = legende_parametres),
col.legend = tm_legend(title = "Valeur de p (norm.) pour le \ncoefficient couverture végétale",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top")
)
) +
tm_shape(data_airbnb) +
tm_dots(size = .1)
tm_shape(mask(raster_metro, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0, 0.05, 0.1, 0.2, 0.3, 1),
values = colors,
label.format = legende_parametres),
col.legend = tm_legend(title = "Valeur de p (norm.) pour le \ncoefficient métro à 500 m",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top")
)
) +
tm_shape(metro) +
tm_lines(col = 'route_name',
lwd = 4,
col.scale = tm_scale_categorical(
values = metro_colors),
col.legend = tm_legend(title = "Ligne de métro",
frame = FALSE,
position = tm_pos_in(pos.h = "left", pos.v = "top")
)
) +
tm_shape(data_airbnb) +
tm_dots(size = .1)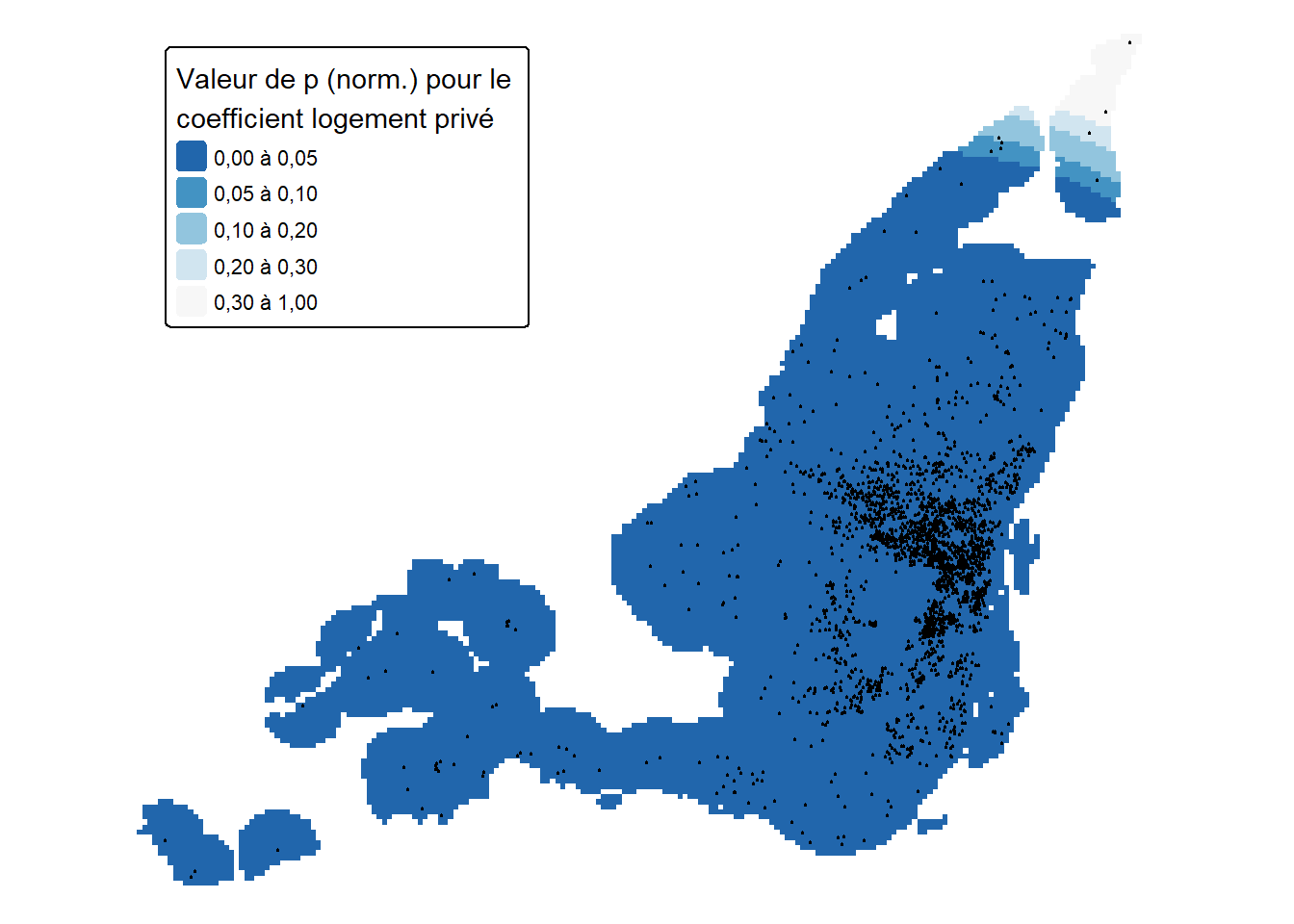
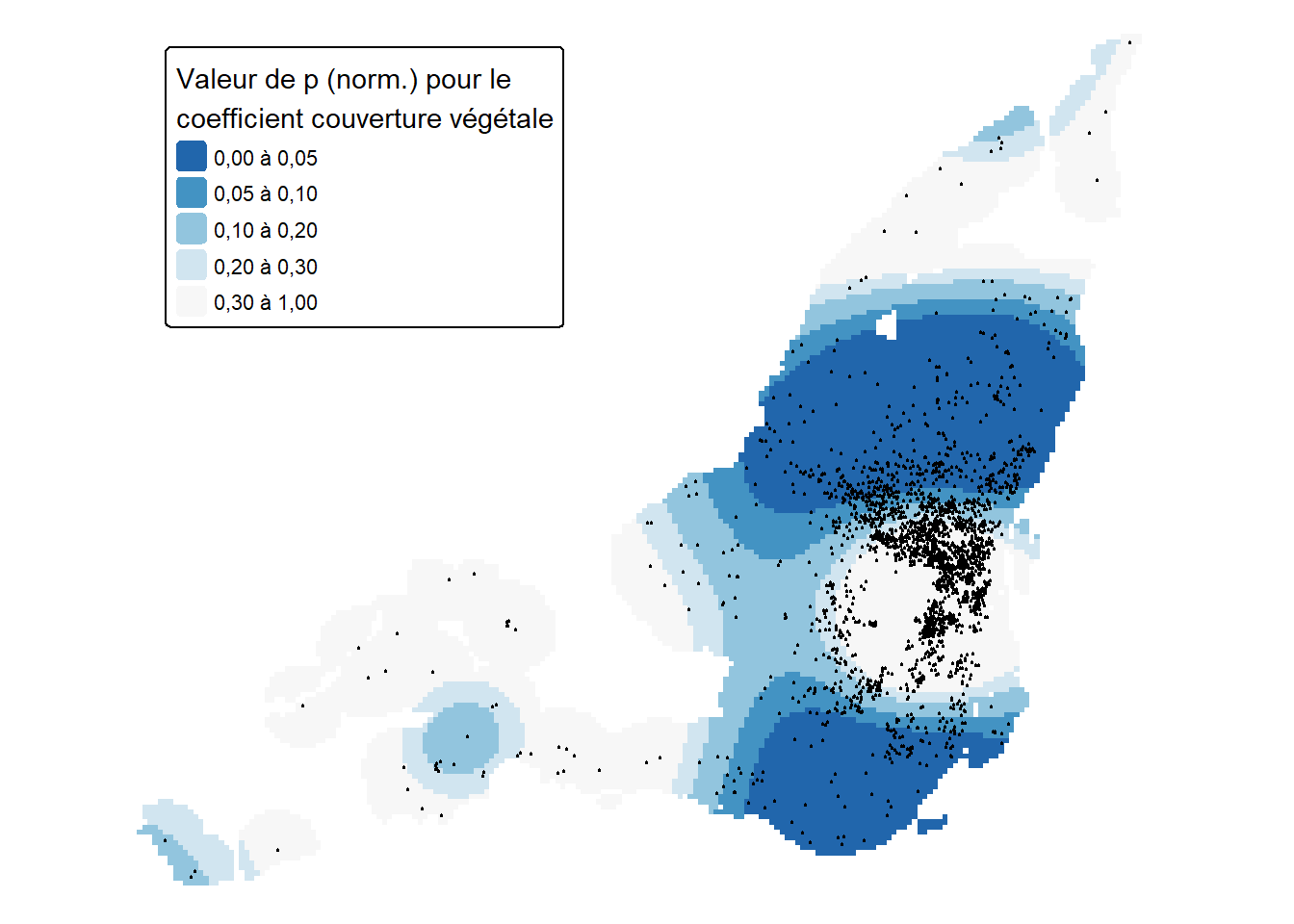
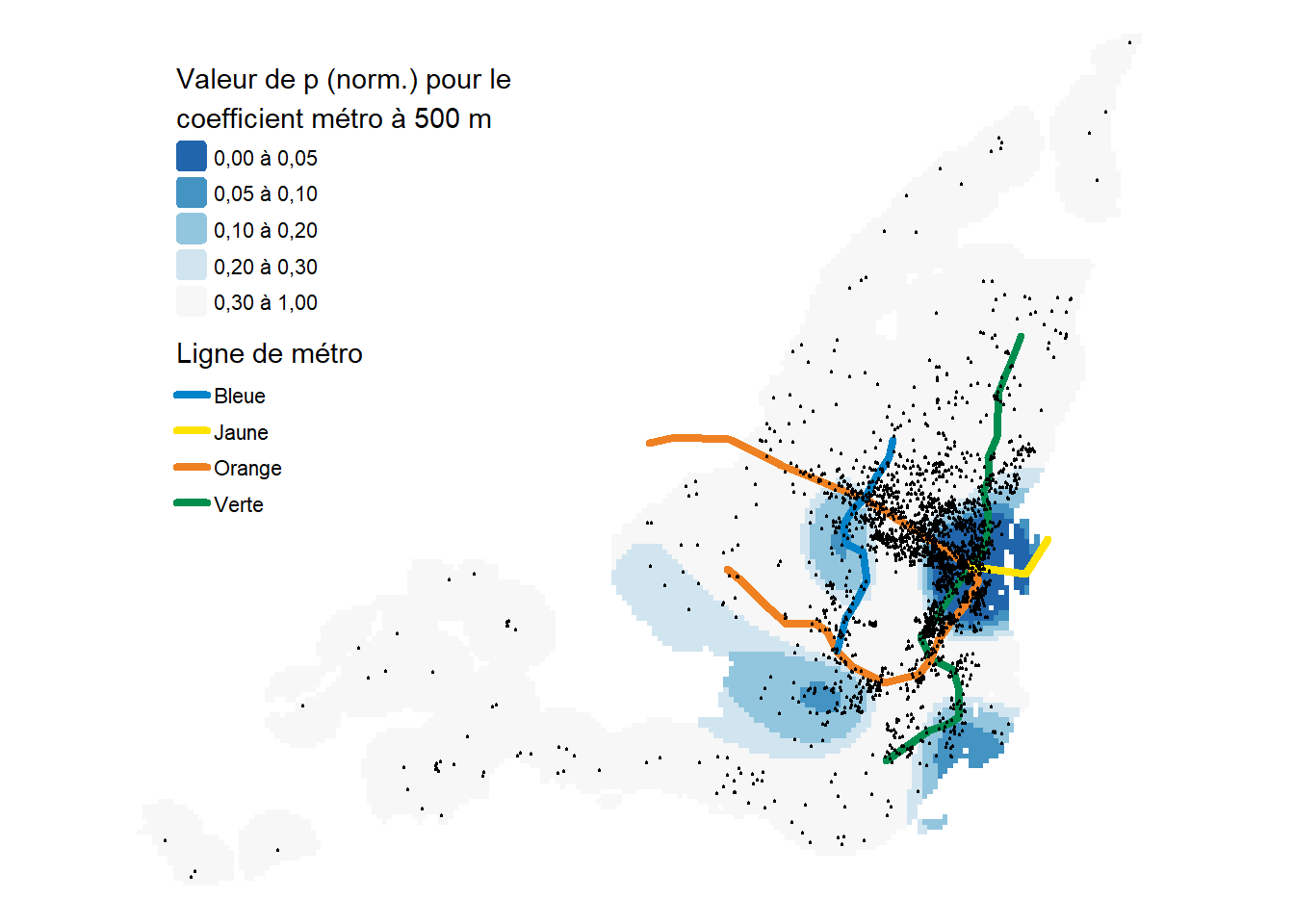
La seconde consiste à obtenir des valeurs de p avec une approche par simulation, soit une approche bayésienne qui consiste à échantillonner des valeurs des coefficients à partir de leurs distributions postérieures.
# Complétion du dataframe de prédiction
pred_df <- coords
pred_df$private <- 1
pred_df$bedrooms <- 0
pred_df$stationnement_gratuit <- 0
pred_df$jardin_ou_cours <- 0
pred_df$number_of_reviews <- 0
pred_df$review_scores_rating <- 0
pred_df$super_hote <- 0
pred_df$prt_veg_500m <- 25
pred_df$metro_500m <- 1
# Extraction des échantillons des valeurs des distributions postérieures
# des effets non linéaires de notre modèle.
# Nous devons ensuite compter le nombre de fois ou les valeurs échantillonées
# étaient positives ou négatives au cours des simulations.
df_sign <- pred_df %>%
add_smooth_samples(model3, n = 2500) %>%
fgroup_by(.row, .term) %>%
fsummarise(
p_inf0 = fsum(.value < 0) / fmax(.draw),
p_sup0 = fsum(.value > 0) / fmax(.draw)) %>%
fmutate(
pval = 1-(pmax(p_inf0, p_sup0))
) %>%
fmutate(
pval = ifelse(p_inf0 > p_sup0, pval * -1, pval)
) %>%
pivot(how = 'wider', values = c('pval'), ids = c('.row'), names = '.term')
# Récupération des valeurs de p
pred_df$sign_metro_500m <- df_sign[['s(X,Y):metro_500m']]
pred_df$sign_private <- df_sign[['s(X,Y):private']]
pred_df$sign_prt_veg_500m <- df_sign[['s(X,Y):prt_veg_500m']]
# Conversion des prédictions en objets raster pour la cartographie
vars <- c(c("X", "Y","sign_private", "sign_metro_500m","sign_prt_veg_500m"))
data_rast <- as.matrix(pred_df[, vars])
raster_private <- rast(data_rast[,c(1,2,3)],type = 'xyz')
crs(raster_private) <- crs(data_airbnb)
raster_veg <- rast(data_rast[,c(1,2,5)],type = 'xyz')
crs(raster_veg) <- crs(data_airbnb)
raster_metro <- rast(data_rast[,c(1,2,4)],type = 'xyz')
crs(raster_metro) <- crs(data_airbnb)
colors <- rev(c('#F7F7F7','#D1E5F0', '#92C5DE', '#4393C3', '#2166AC'))
tmap_options(frame = FALSE)
tm_shape(mask(raster_private, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0, 0.05, 0.1, 0.2, 0.3, 1),
values = colors,
label.format = legende_parametres),
col.legend = tm_legend(title = "Valeur de p (sim.) pour le \ncoefficient logement privé",
position = tm_pos_in(pos.h = "left", pos.v = "top"),
frame = FALSE
)
) +
tm_shape(data_airbnb) + tm_dots(size = .1)
tm_shape(mask(raster_veg, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0, 0.05, 0.1, 0.2, 0.3, 1),
values = colors,
label.format = legende_parametres),
col.legend = tm_legend(title = "valeur de p (sim.) pour le \ncoefficient couverture végétale",
position = tm_pos_in(pos.h = "left", pos.v = "top"),
frame = FALSE
)
) +
tm_shape(data_airbnb) + tm_dots(size = .1)
tm_shape(mask(raster_metro, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
breaks = c(0, 0.05, 0.1, 0.2, 0.3, 1),
values = colors,
label.format = legende_parametres),
col.legend = tm_legend(title = "Valeur de p (sim.) pour le \ncoefficient métro à 500 m",
position = tm_pos_in(pos.h = "left", pos.v = "top"),
frame = FALSE
)
) +
tm_shape(metro) +
tm_lines(col = 'route_name',
lwd = 4,
col.scale = tm_scale_categorical(
values = metro_colors),
col.legend = tm_legend(title = "Ligne de métro",
position = tm_pos_in(pos.h = "left", pos.v = "top"),
frame = FALSE
)
) +
tm_shape(data_airbnb) + tm_dots(size = .1)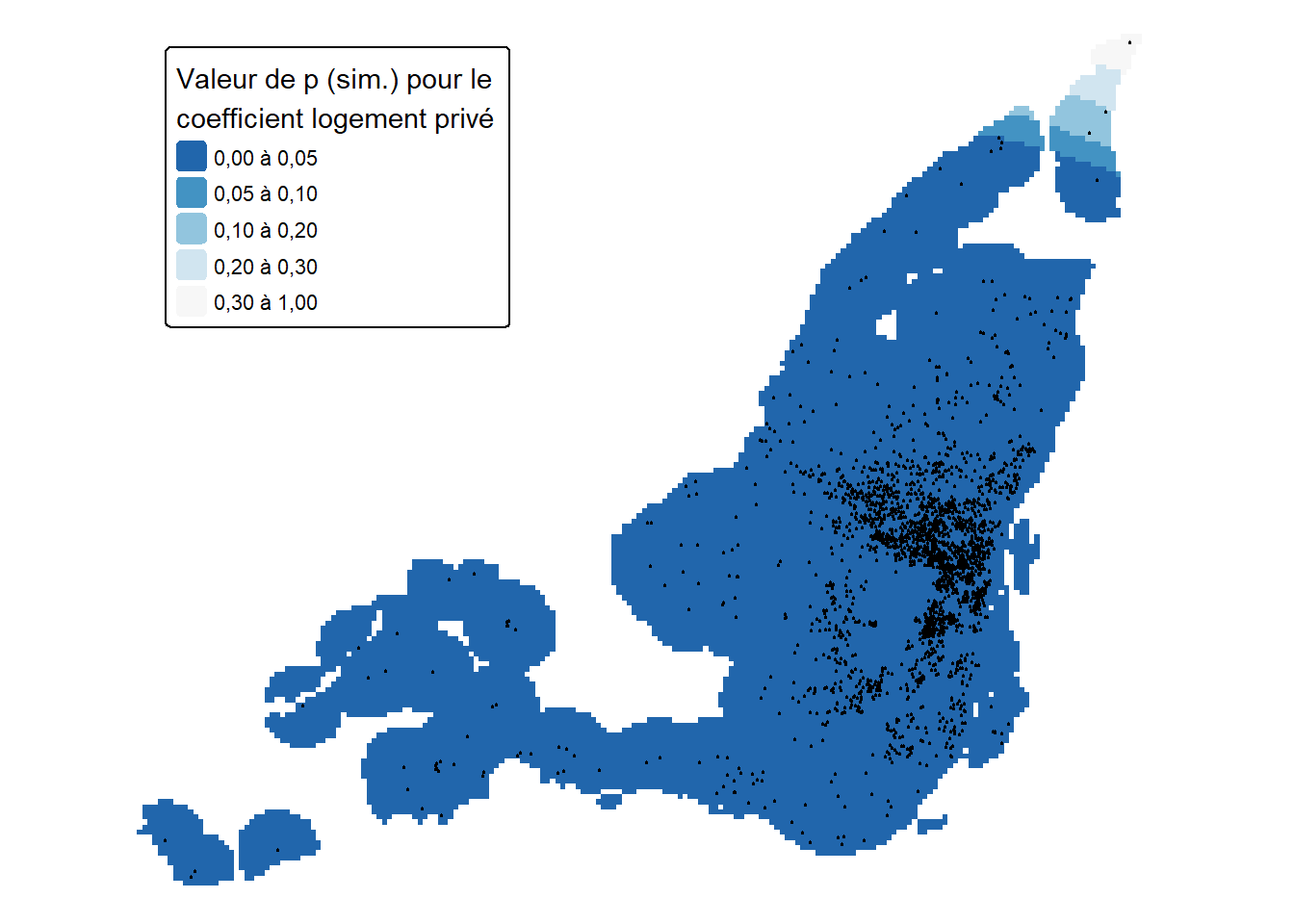
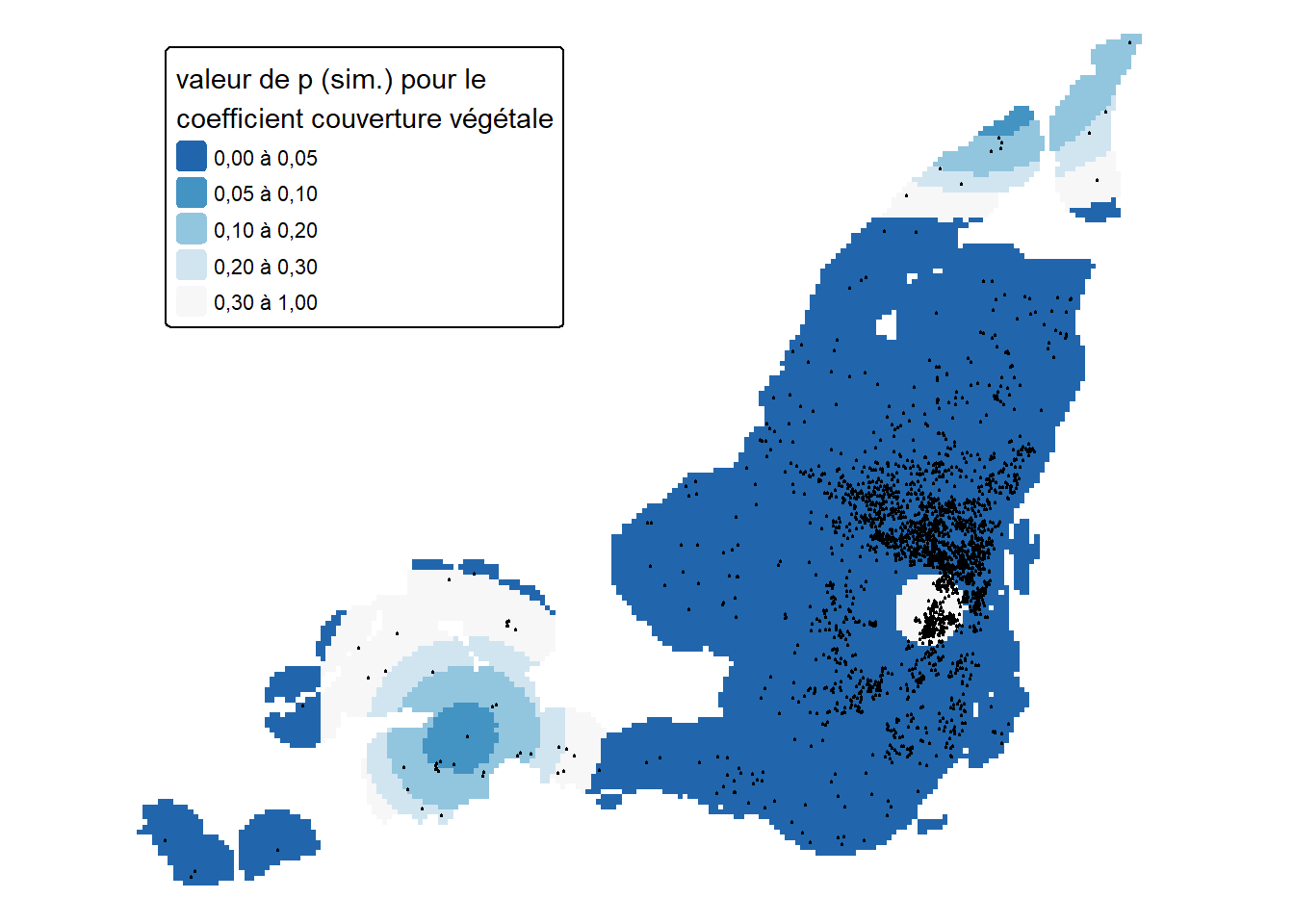
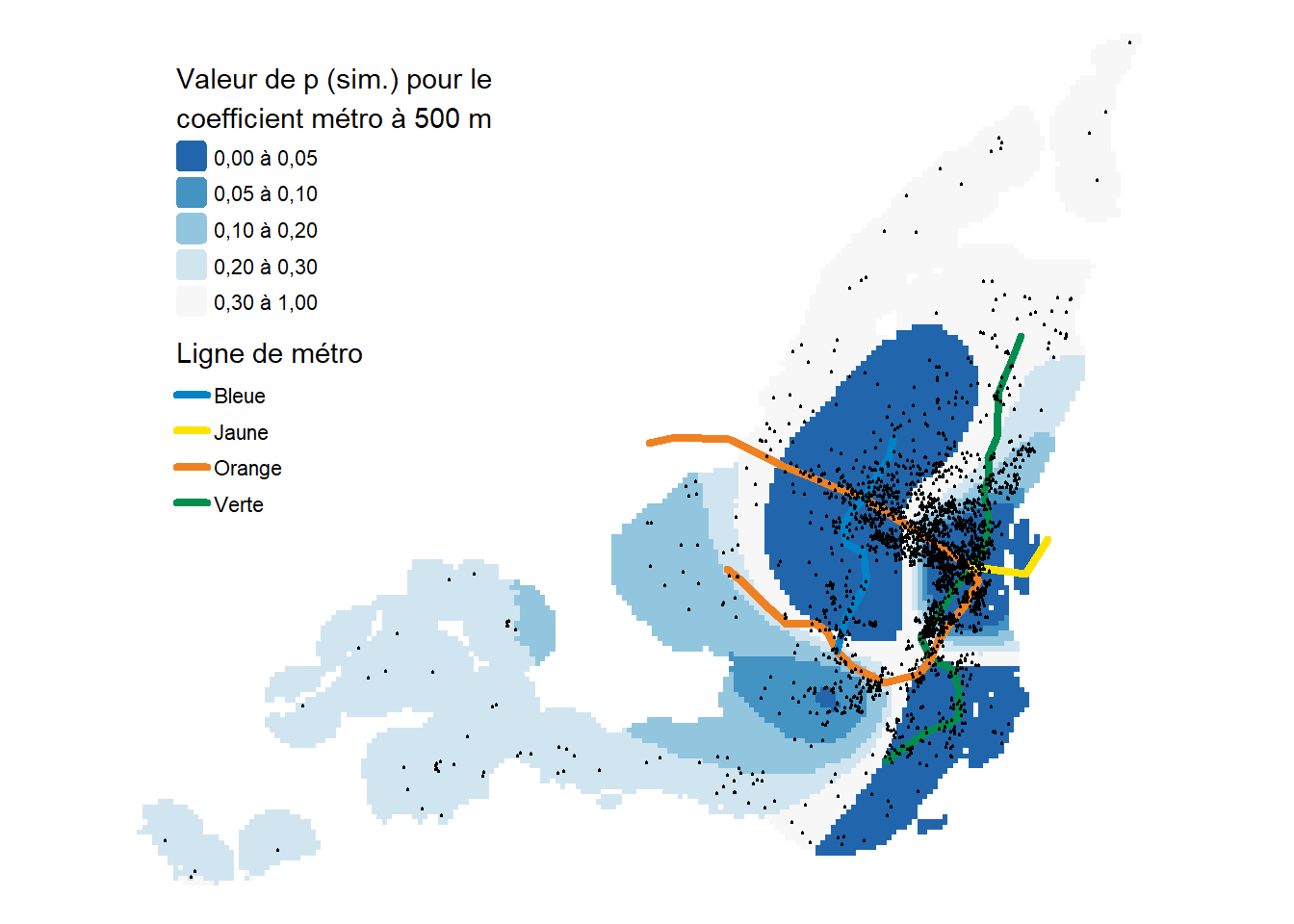
Les cartes des figures 10.4 à 10.9 illustrent la distribution spatiale des valeurs de p de nos splines (normales et simulées) faisant varier localement les coefficients. Il est important d’utiliser leurs résultats afin de déterminer si les effets observés aux figures 10.1 à 10.3 sont significativement différents de zéro.
10.2 Modèles linéaires généralisés à effets mixtes (GLMM)
Dans cette section, nous expliquons comment utiliser un effet aléatoire pour permettre à un coefficient de varier spatialement dans un modèle GLMM. Pour un rappel sur les GLMM et les effets aléatoires, vous pouvez consulter le chapitre sur les GLMM du livre Méthodes quantitatives en sciences sociales : un grand bol d’R (Apparicio et Gelb 2022). Vous pouvez également relire la section 2.3 de ce manuel dans laquelle nous avons expliqué comment un effet aléatoire peut être utilisé pour modéliser un effet spatial.
10.2.1 Effets aléatoires et coefficients variant spatialement
À titre de rappel, un effet aléatoire dans un modèle est un terme dont nous supposons que les valeurs proviennent d’une distribution normale. La forme la plus courante d’un effet aléatoire est la constante aléatoire, permettant de contrôler les effets de groupes. En effet, il est primordial de contrôler le fait que deux observations provenant d’un même groupe ou plus de chances de ressembler que deux observations provenant de groupes différents. Dans la section 2.3, nous avons montré comment introduire une structure de covariance spatiale (CAR, Matérn, exponentielle, etc.) pour un effet aléatoire. Cette structure permet ainsi de tenir compte du fait que deux observations proches spatialement ont plus de chance de se ressembler que deux observations lointaines.
Nous avions notamment formulé le GLMM suivant :
\[ \begin{aligned} &y \sim Normal(\mu, \sigma) \\ &\mu = \beta_0 + \beta X + \nu\\ &\nu \sim N(0,\Omega) \end{aligned} \tag{10.3}\]
Dans le modèle décrit à l’équation 10.3, \(\nu\) correspond à un effet aléatoire et \(\Omega\) une matrice de covariance spatiale. Ainsi, \(\nu\) peut être vu comme une série de bonus et de malus spatialement autocorrélés accordés à la constante du modèle. Il est tout à fait possible d’étendre cette spécification pour ne pas faire varier que la constante, mais aussi certains coefficients du modèle.
\[ \begin{aligned} &y \sim Normal(\mu, \sigma) \\ &\mu = \beta_0 + \sum^k_{i=1} \beta_i X_i + \sum^l_{ j=1} [(\beta_j + \eta_j)X_j] + \nu \\ &\nu \sim N(0,\Omega) \\ &\eta_j \sim N(0,\Phi_j) \end{aligned} \tag{10.4}\]
Avec :
- \(k\), les variables dont les effets sont fixes et ne varient pas dans l’espace.
- \(l\), les variables dont les effets varient dans l’espace.
- \(\eta_j\) un effet aléatoire provenant d’une distribution normale centrée sur 0 et suivant une structure d’autocorrélation spatiale \(\Phi_j\). Puisque cet effet est centré sur 0, \(\beta_j\) représente l’effet moyen attendu du coefficient sur l’ensemble du territoire. Les valeurs de \(\eta_j\) correspondent donc à des bonus ou malus locaux qui viennent renforcer ou réduire l’effet de \(\beta_j\).
Les effets aléatoires que nous avions observés dans la section 2.3 (car, matérn, exponentiel, sphérique, etc.) peuvent être utilisés pour paramétrer \(\Omega\) et \(\Phi\) en fonction de la relation spatiale à modéliser (distance ou contiguïté) et selon leur adéquation aux données. Notez que puisque nos effets aléatoires spatiaux proviennent de distributions normales multivariées, ils sont souvent appelés des processus gaussiens.
Il est toujours préférable d’utiliser un modèle moins complexe pour décrire un phénomène (principe de parcimonie). Il est donc essentiel de s’assurer que l’ajout de coefficients variant spatialement se justifie dans un modèle. Pour cela, il est possible d’utiliser l’AIC ou d’autres critères similaires (BIC, DIC, REML). Il est aussi important de vérifier si la variance estimée de ces effets aléatoires est significativement différente de zéro. En effet, si ce n’est pas le cas, cela signifie que l’effet aléatoire n’a essentiellement aucune variance et donc aucun impact dans le modèle.
Variance d’un effet aléatoire et valeurs estimées
Le fait que la variance d’un effet aléatoire est différente de zéro ne signifie pas pour autant que les valeurs estimées de cet effet aléatoire sont significativement différentes de zéro.
Dans le cas des GLMM avec coefficients variant spatialement, nous formulons l’hypothèse que la variation locale d’un coefficient provient d’un processus gaussien spatial. La variance de ce processus gaussien peut être significativement différente de zéro, mais les réalisations de ce processus peuvent ne pas être significativement différentes de zéro. En d’autres termes, les bonus et malus locaux des coefficients peuvent être tellement faibles et incertains que leurs contributions finales au modèle sont anecdotiques, et ce, même si la variance de l’effet aléatoire est significative. Il est donc important lorsque l’on cartographie les coefficients variant spatialement de bien indiquer où ceux-ci sont significativement différents de zéro. Il s’agit exactement du même enjeu qu’avec les splines spatiales présentées plus tôt.
Prenons un exemple avec un modèle fictif. Admettons que pour ce modèle, nous avons estimé un coefficient fixe \(\beta_j = 0.5\) qui est significatif au seuil de \(p < 0.01\). Ce coefficient représente l’effet moyen de la variable \(j\) quand nous ne savons pas où nous nous trouvons sur le territoire, soit l’effet moyen sur l’ensemble du territoire. Admettons aussi que nous avons estimé un effet aléatoire suivant un processus gaussien spatial dont la variance est de \(\sigma = 0.1\) et que cette variance est significativement différente de zéro. Pour un emplacement \(i\), notre modèle a déterminé que la valeur de l’effet aléatoire est de \(\eta_j = 0.05\), mais que cet effet n’est pas significativement différent de zéro avec \(p = 0.15\). Le coefficient au point \(i\) peut être calculé par la simple somme des deux effets : \(\beta_{ji} = \beta_j + \eta_j\), mais il ne sera pas statistiquement différent de \(\beta_j\) puisque \(\eta_j\) n’est pas lui-même significativement différent de zéro.
Il serait aussi possible d’avoir une situation différente dans laquelle \(\beta_j\) n’est pas significatif : \(\beta_j = 0.05\) avec \(p = 0.35\). Dans cette situation, l’effet général de \(\beta_j\) est proche de zéro sur l’ensemble du territoire. Admettons maintenant que \(\eta_j = 0.15\) avec \(p < 0.01\). Cela signifierait que pour le point du territoire \(i\), l’effet de la variable \(j\) est \(x_j \times(\beta_j + \eta_j)\). Cependant, puisque l’effet général \(\beta_j\) n’est pas différent de zéro, alors il est possible de dire que l’effet local est uniquement dû à \(\eta_j\).
10.2.2 Mise en œuvre dans R
Pour illustrer comment des effets aléatoires peuvent être utilisés pour faire varier spatialement les coefficients d’un modèle, nous allons reprendre l’exemple des décès attribués à la Covid-19 aux États-Unis. Nous tenterons d’améliorer le modèle GLMM présenté à la section 2.3.2.
Il existe actuellement assez peu de packages R pour ajuster ce type de modèle. spBayes et INLA sont très flexibles, mais utilisent des méthodes d’ajustement bayésiennes que nous ne couvrons pas dans ce livre. Pour les méthodes fréquentistes, les choix sont assez limités avec les packages varycoef et sdmTMB. Le premier ne permet pas d’ajuster des GLM et se limite à des modèles linéaires classique (family = gaussian). Par conséquent, nous utiliserons ici uniquement le package sdmTMB.
Puisque l’estimation d’effets aléatoires spatiaux est relativement coûteuse en temps de calcul, sdmTMB utilise une stratégie relativement récente (Stochastic Partial Differential Equation) consistant à approximer ces effets aléatoires (Lindgren, Rue et Lindström 2011). L’idée générale est de découper la zone d’étude en un ensemble de triangles (mesh) dont les extrémités sont appelées des nœuds (oui, comme pour une spline). L’effet aléatoire spatial est estimé pour chaque nœud, et les valeurs entre les nœuds sont ensuite calculées par interpolation bilinéaire. Ces effets aléatoires suivent des processus gaussiens discrets (Markov random field) avec des matrices de covariance suivant une structure Matérn. Cette méthode d’estimation est particulièrement efficace, car elle simplifie grandement le calcul de l’effet aléatoire. Le processus gaussien continu (gaussian field) est approximé par un processus gaussien discret (gaussian markov random field). Cette formulation permet de limiter la dépendance spatiale continue à une dépendance spatiale de voisinage, ce qui réduit considérablement la taille des matrices à manipuler pour estimer les effets aléatoires.
Pour faciliter l’ajustement du modèle avec sdmTMB, il est nécessaire que les différentes variables continues soient centrées et réduites. Nous allons également transformer les coordonnées géographiques en dizaines de kilomètres. Il est également nécessaire de créer une mesh. Cette dernière doit être suffisamment précise pour résumer efficacement les relations spatiales étudiées. Cependant, plus la mesh est fine, plus le temps de calcul est important, car plus le nombre d’effets aléatoires à estimer est grand.
library(sf, quietly = TRUE)
library(ggplot2, quietly = TRUE)
library(tmap, quietly = TRUE)
library(dplyr, quietly = TRUE)
library(spdep, quietly = TRUE)
library(DHARMa, quietly = TRUE)
library(sdmTMB, quietly = TRUE)
# Chargement des données
covid_data <- readRDS('data/chap02/covid_usa.rds')
# Recodage des valeurs négatives pour le nombre de décès
covid_data$deaths_3 <- ifelse(covid_data$deaths_3 < 0,
0,
covid_data$deaths_3
)
# Conservation des comtés uniques
covid_data <- covid_data %>%
group_by(FIPS) %>%
slice_head(n = 1)
data_mode1 <- na.omit(covid_data)
# Récupération et mise à l'échelle des coordonnées spatiales
XY <- st_coordinates(st_centroid(data_mode1))
data_mode1$X <- XY[,1] / 10000
data_mode1$Y <- XY[,2] / 10000
# Standardisation des différentes variables quantitatives
vars <- c('income', 'income', 'per_black', 'per_hispanic', 'per_atleast_hs',
'per_nursing', 'X65plus','political_leaning', 'strict_p3',
'mask_usage_p3', 'google_p3', 'dist_to_airport', 'density')
for(var in vars){
data_mode1[[paste0('cr_', var)]] <-
scale(data_mode1[[var]], center = TRUE, scale = TRUE)
}
# Mise en logarithme de la population pour l'utiliser comme offset
data_mode1$population_log <- log(data_mode1$population)
# Réalisation de la mesh, le paramètre cutoff contrôle la longueur
# minimale des cotés des triangles
mesh1 <- make_mesh(st_drop_geometry(data_mode1), c('X', 'Y'), cutoff = 20)
mesh2 <- make_mesh(st_drop_geometry(data_mode1), c('X', 'Y'), cutoff = 1)
mesh3 <- make_mesh(st_drop_geometry(data_mode1), c('X', 'Y'), cutoff = 5)
plot(mesh1)
plot(mesh2)
plot(mesh3)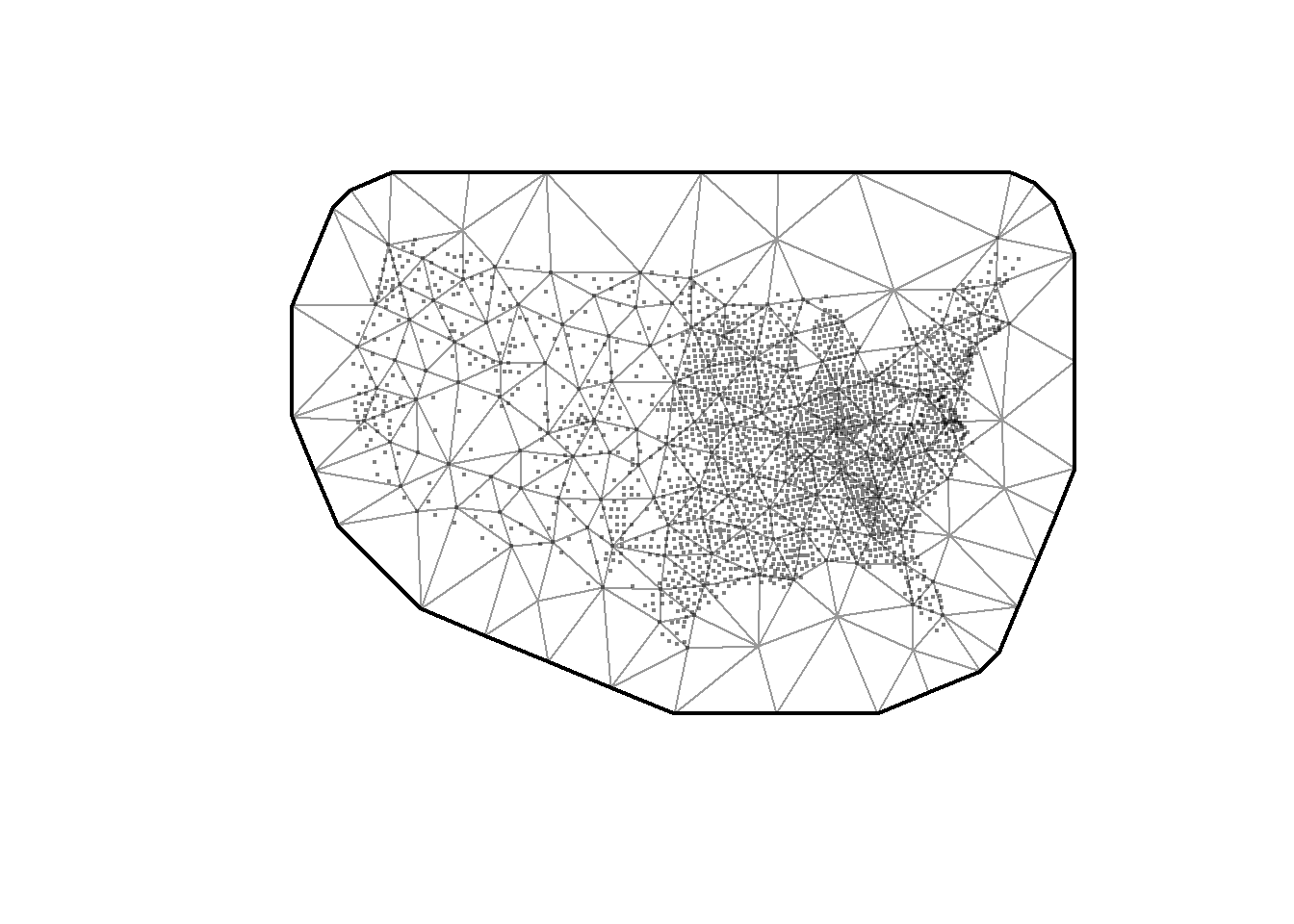
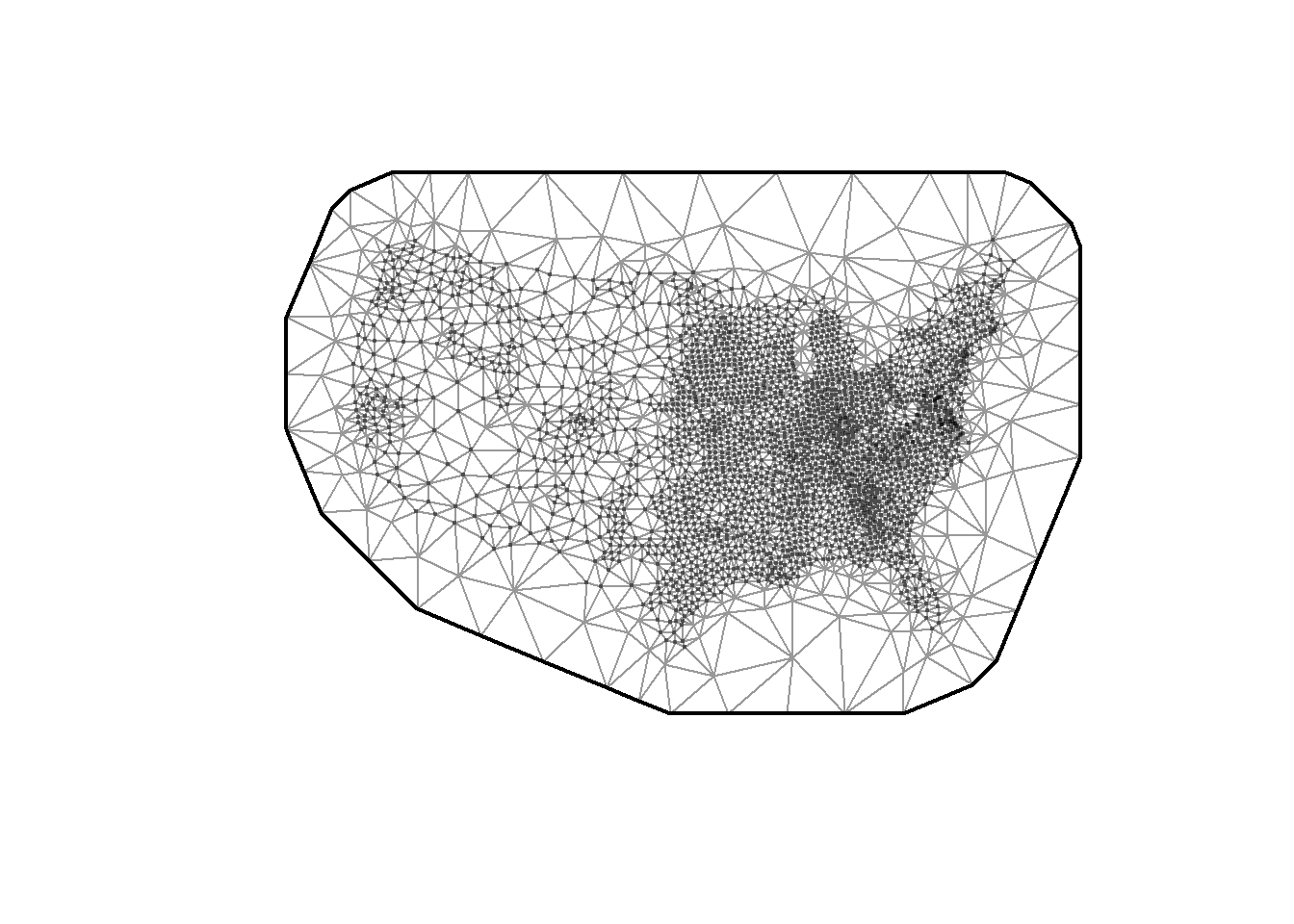
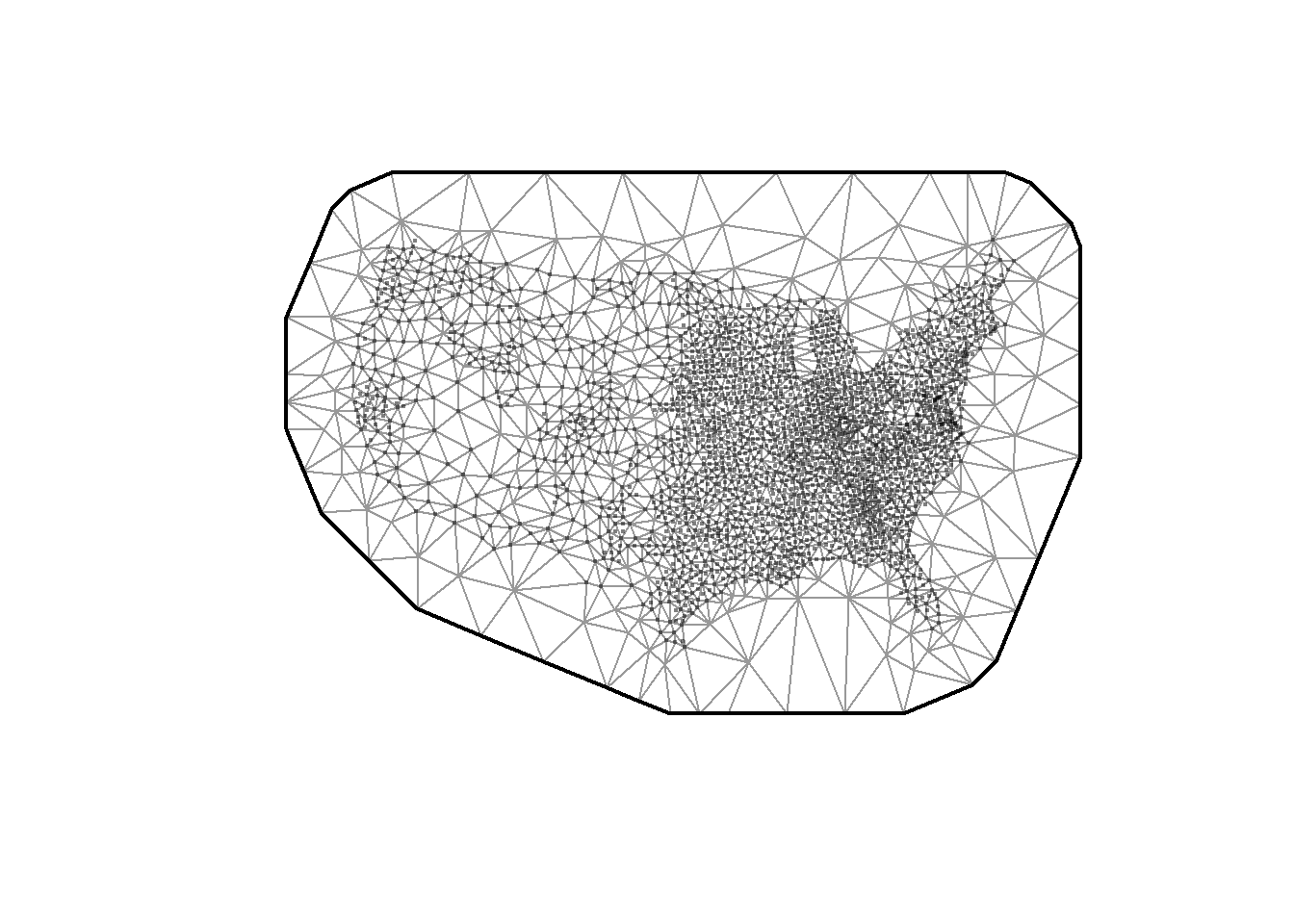
Maintenant que nous disposons de notre mesh et que nous avons appliqué les transformations aux données, nous ajustons un modèle de référence dans lequel aucun coefficient ne varie spatialement. Nous avons seulement une constante spatiale, comme réalisé dans la section 2.3.2.
# Calcul d'un modèle nul qui sera utilisé pour calculer les différents
# pseudos R2
model0 <- sdmTMB(
data = st_drop_geometry(data_mode1),
formula = deaths_3 ~ 1,
offset = 'population_log',
family = nbinom2 (link = "log"),
spatial = FALSE
)
# Définition d'une fonction pour calculer les pseudo R2
rsqs <- function(loglike.full,
full.deviance,
loglike.null,
null.deviance,
nb.params, n){
explained_dev <- 1-(full.deviance / null.deviance)
K <- nb.params
r2_faddenadj <- 1- (loglike.full - K) / loglike.null
Lm <- loglike.full
Ln <- loglike.null
Rcs <- 1 - exp((-2/n) * (Lm-Ln))
Rn <- Rcs / (1-exp(2*Ln/n))
return(
list("deviance expliquee" = explained_dev,
"MacFadden ajuste" = r2_faddenadj,
"Cox and Snell" = Rcs,
"Nagelkerke" = Rn
)
)
}
# Calcul du premier modèle avec uniquement la constante variant spatialement
model1 <- sdmTMB(
data = st_drop_geometry(data_mode1),
formula = deaths_3 ~
cr_income + cr_per_black + cr_per_hispanic + cr_per_atleast_hs +
cr_per_nursing + cr_X65plus +
cr_political_leaning + cr_strict_p3 +
cr_mask_usage_p3 + cr_google_p3 + cr_dist_to_airport + cr_density,
offset = 'population_log',
mesh = mesh3,
family = nbinom2 (link = "log"),
spatial = TRUE
)
r2_model1 <- rsqs(
loglike.full = as.numeric(logLik(model1)),
loglike.null = as.numeric(logLik(model0)),
full.deviance = deviance(model1),
null.deviance = deviance(model0),
nb.params = cAIC(model1, what = 'edf')[[1]],
n = nrow(data_mode1)
)
# Analyse des résidus simulés du modèle
simulations <- simulate(model1, nsim = 500, type = "mle-mvn")
resids <- dharma_residuals(simulations, model1, return_DHARMa = TRUE)
plot(resids)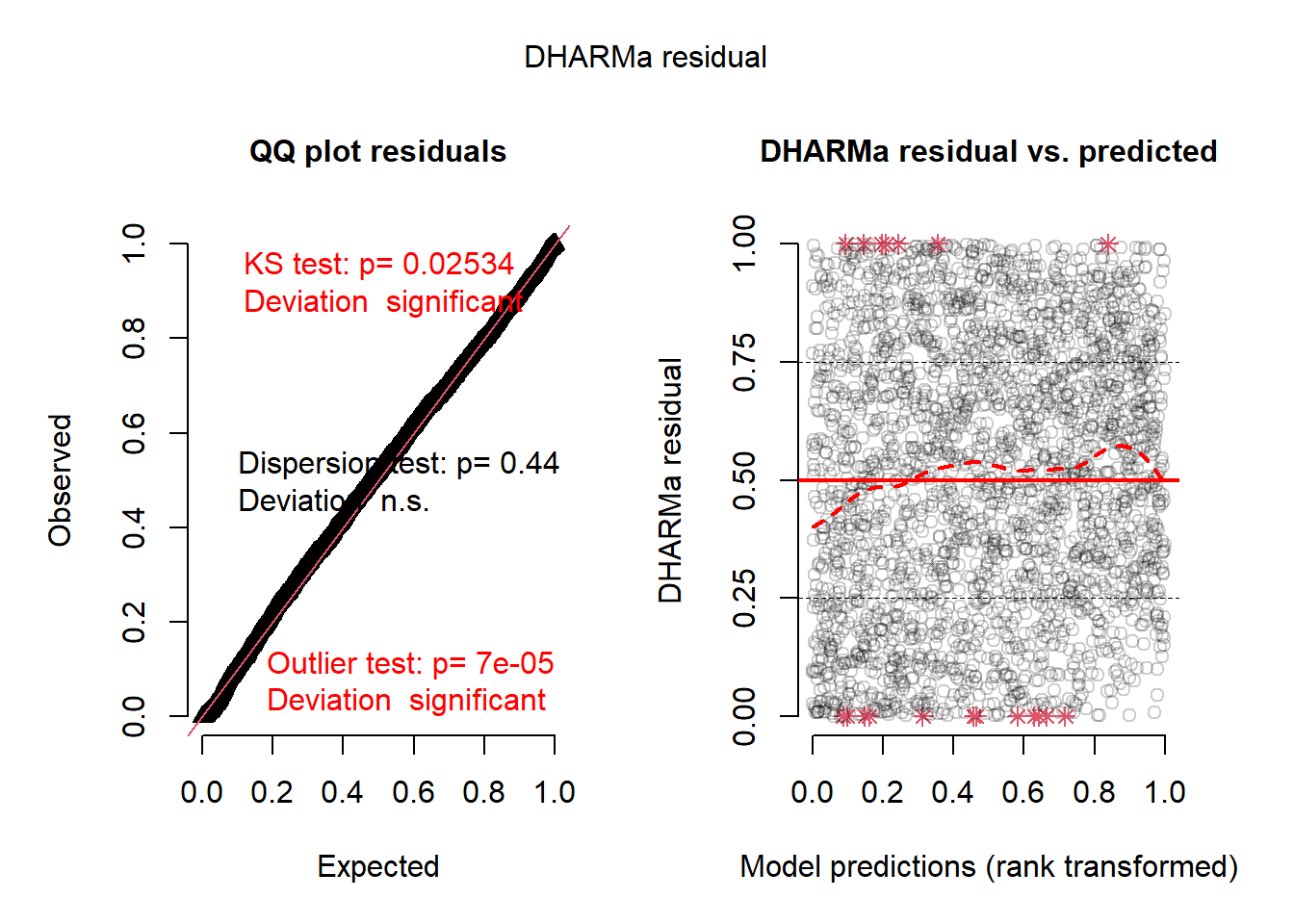
La figure 10.13 indique que les résidus simulés du modèle sont relativement proches d’une distribution uniforme. Il y a toutefois quelques valeurs extrêmes.
print(r2_model1)$`deviance expliquee`
numeric(0)
$`MacFadden ajuste`
[1] 0.05679213
$`Cox and Snell`
[1] 0.5529029
$Nagelkerke
[1] 0.5529539Les pseudos R2 du modèle sont relativement faibles, indiquant qu’une partie non négligeable du phénomène reste inexpliqué par le modèle.
df_pred <- data.frame(
y = data_mode1$deaths_3 / data_mode1$population,
pred1 = predict(model1, type = 'response')$est
)
ggplot(df_pred) +
geom_point(aes(x = y, y = pred1)) +
geom_abline(slope = 1, intercept = 0, color = 'red', linetype = 'dashed') +
labs(x = 'Taux de décès réel',
y = 'Taux de décès prédit'
) +
theme_bw()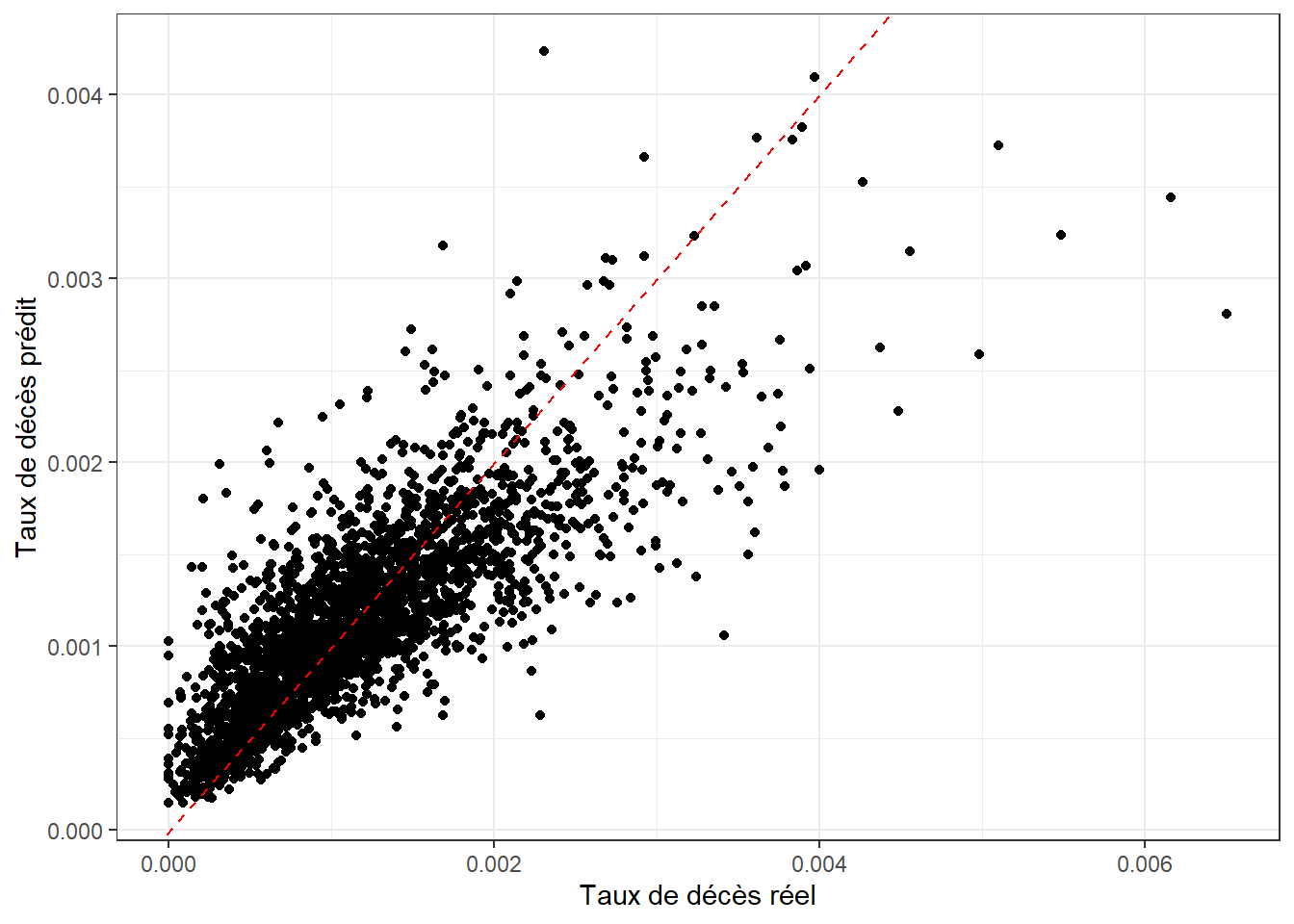
La figure 10.14 montre que le modèle parvient tout de même à effectuer des prédictions qui se rapprochent des valeurs réelles.
Nous considérons ici plusieurs coefficients pouvant avoir un effet variant spatialement. Par exemple, l’intensité des inégalités socio-économiques varie d’un État à l’autre, ce qui pourrait se traduire par des effets plus ou moins prononcés des variables socio-économiques. Les variables sur l’application des mesures sanitaires ou sur la mobilité sont de moins bonne qualité, nous éviterons donc de les faire varier spatialement pour éviter des risques de surinterprétation. La distance à l’aéroport le plus proche pourrait aussi avoir un effet variant spatialement, car tous les aéroports n’ont probablement pas eu la même contribution lors de la pandémie.
Nous construisons ainsi un modèle avec ces différents effets pour ensuite retirer ceux qui ne sont pas significatifs.
model2 <- sdmTMB(
data = st_drop_geometry(data_mode1),
formula = deaths_3 ~
cr_income + cr_per_black + cr_per_hispanic + cr_per_atleast_hs +
cr_per_nursing + cr_X65plus +
cr_political_leaning + cr_strict_p3 +
cr_mask_usage_p3 + cr_google_p3 + cr_dist_to_airport + cr_density,
offset = 'population_log',
mesh = mesh3, # can be omitted for a non-spatial model
spatial = TRUE,
spatial_varying = ~ 1 + cr_X65plus + cr_per_atleast_hs +
cr_income + cr_per_black + cr_per_hispanic +
cr_per_nursing + cr_dist_to_airport,
family = nbinom2 (link = "log")
)vars <- c("range", "phi", "constante", model2$spatial_varying)
tableau <- tidy(model2, effects = 'ran_pars', conf.int = TRUE) %>%
as.data.frame()
tableau$term <- vars
knitr::kable(tableau, digits = 3,
col.names = c("terme", "coef.", "err. stand.", "IC 2,5 %", "IC 97,5 %"),
format.args = list(decimal.mark = ',', big.mark = " "))| terme | coef. | err. stand. | IC 2,5 % | IC 97,5 % |
|---|---|---|---|---|
| range | 62,384 | 9,107 | 46,861 | 83,049 |
| phi | 11,455 | 0,601 | 10,336 | 12,695 |
| constante | 0,419 | 0,043 | 0,342 | 0,513 |
| cr_X65plus | 0,111 | 0,019 | 0,080 | 0,155 |
| cr_per_atleast_hs | 0,087 | 0,026 | 0,049 | 0,155 |
| cr_income | 0,082 | 0,024 | 0,047 | 0,145 |
| cr_per_black | 0,000 | 0,022 | 0,000 | Inf |
| cr_per_hispanic | 0,000 | 0,020 | 0,000 | Inf |
| cr_per_nursing | 0,105 | 0,028 | 0,063 | 0,176 |
| cr_dist_to_airport | 0,000 | 0,066 | 0,000 | Inf |
Le tableau 10.2 indique clairement que trois de nos sept coefficients spatiaux n’ont pas de variation spatiale significative (IC 2,5 % < 0.01). Nous allons donc réajuster le modèle en retirant ces trois termes (cr_dist_to_airport, cr_per_hispanic, cr_per_black).
model2 <- sdmTMB(
data = st_drop_geometry(data_mode1),
formula = deaths_3 ~
cr_income + cr_per_black + cr_per_hispanic + cr_per_atleast_hs +
cr_per_nursing + cr_X65plus +
cr_political_leaning + cr_strict_p3 +
cr_mask_usage_p3 + cr_google_p3 + cr_dist_to_airport + cr_density,
offset = 'population_log',
mesh = mesh3, # can be omitted for a non-spatial model
spatial = TRUE,
spatial_varying = ~ 1 + cr_X65plus + cr_per_atleast_hs +
cr_income + cr_per_nursing ,
family = nbinom2 (link = "log")
)# Analyse des résidus simulés du modèle
simulations <- simulate(model2, nsim = 500, type = "mle-mvn")
resids <- dharma_residuals(simulations, model2, return_DHARMa = TRUE)
plot(resids)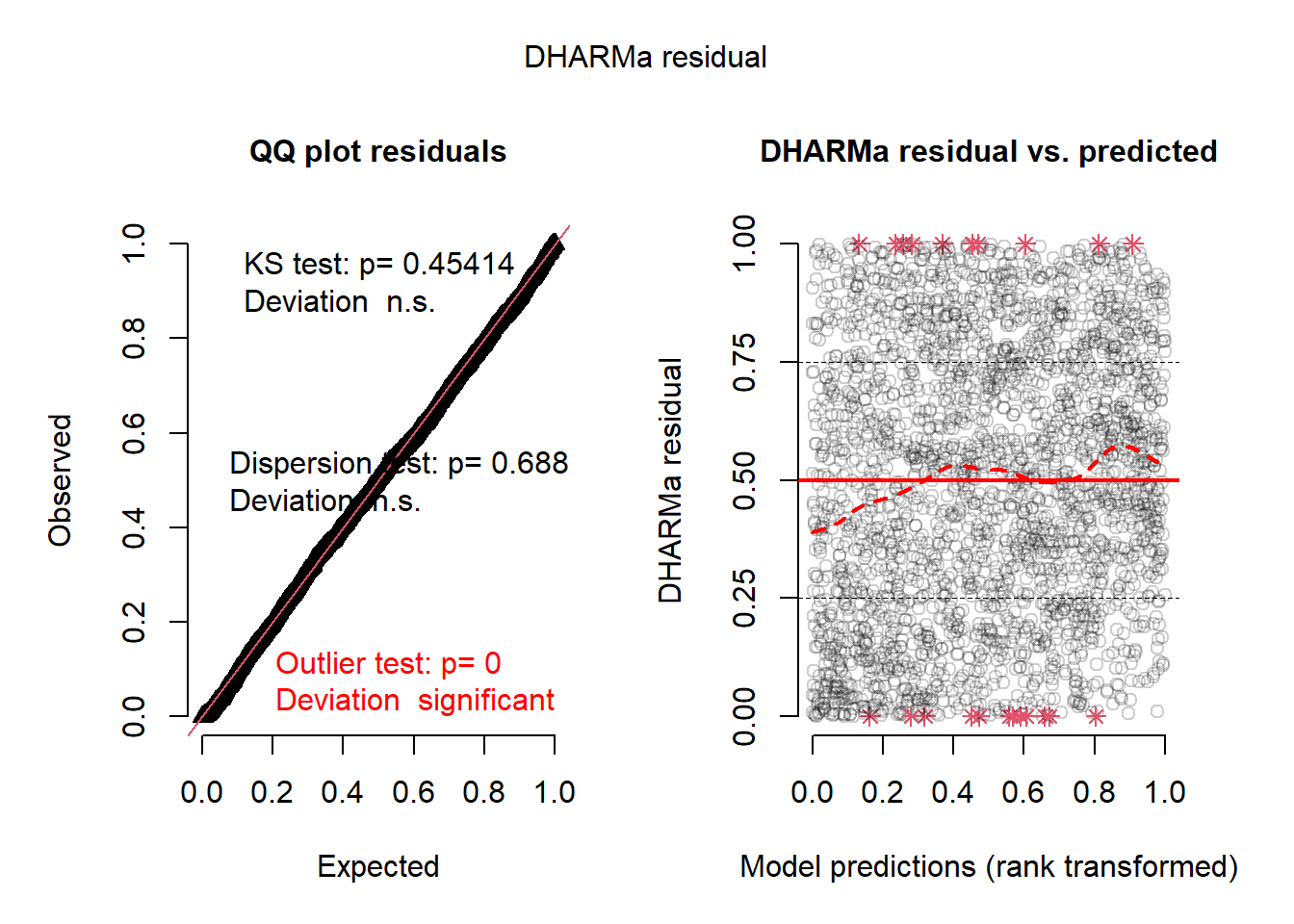
La nouvelle version du modèle incluant nos coefficients variant significativement spatialement obtient également de bons résidus simulés (figure 10.15).
r2_model2 <- rsqs(
loglike.full = as.numeric(logLik(model2)),
loglike.null = as.numeric(logLik(model0)),
full.deviance = deviance(model2),
null.deviance = deviance(model0),
nb.params = cAIC(model2, what = 'edf')[[1]],
n = nrow(data_mode1)
)
tab_r2 <- data.frame(
r2s = c("MacFadden ajusté", "Cox et Snell", "Nagelkerke"),
model1 = unlist(r2_model1),
model2 = unlist(r2_model2)
)
knitr::kable(tab_r2, digits = 3,
row.names = FALSE,
format.args = list(decimal.mark = ',', big.mark = " "),
col.names = c('R2', 'Modèle 1', 'Modèle 2'))| R2 | Modèle 1 | Modèle 2 |
|---|---|---|
| MacFadden ajusté | 0,057 | 0,067 |
| Cox et Snell | 0,553 | 0,564 |
| Nagelkerke | 0,553 | 0,565 |
En termes de R2, le second modèle n’offre qu’une amélioration très marginale du premier modèle (tableau 10.3).
caic1 <- cAIC(model1)
caic2 <- cAIC(model2)
print(c(caic1, caic2))[1] 22468.75 22371.70L’AIC conditionnel du second modèle est plus petit que celui du premier modèle, indiquant un meilleur ajustement. À titre de rappel, l’AIC conditionnel est une version du AIC plus adaptée pour comparer des modèles à effets mixtes si leurs effets aléatoires sont différents (voir la section 2.3.2).
Nous pouvons à présent analyser les effets fixes du modèle. Pour rappel, les variables indépendantes ont été centrées et réduites. Nous devons donc diviser les coefficients par les écarts types originaux de nos variables indépendantes pour permettre une interprétation dans l’échelle originale des données. Nous devons aussi les mettre en exponentiel afin de pouvoir les interpréter, puisque la fonction de lien est la fonction log.
# Extraction des coefficients et de leur intervalle de confiance
tab_fixe <- tidy(model2, effects = 'fixed', conf.int = TRUE)
# Récupération des écarts types
vars <- c('income', 'income', 'per_black', 'per_hispanic', 'per_atleast_hs',
'per_nursing', 'X65plus','political_leaning', 'strict_p3',
'mask_usage_p3', 'google_p3', 'dist_to_airport', 'density')
sd_values <- sapply(vars, function(x){
sd(data_mode1[[x]])
})
sd_df <- data.frame(
sd = c(1,sd_values),
var = c('(Intercept)', paste0('cr_', vars))
)
# Application des écarts types aux effets estimés
ids <- match(tab_fixe$term, sd_df$var)
tab_fixe$estimate_std <- tab_fixe$estimate
for(col in c("estimate", "conf.low", "conf.high")){
tab_fixe[[col]] <- exp(tab_fixe[[col]] / sd_df$sd[ids])
}
tab_fixe$std.error <- NULL
tab_fixe[1, 1] <- "constante"
knitr::kable(tab_fixe, digits = 3,
format.args = list(decimal.mark = ',', big.mark = " "),
col.names = c('terme','coefficient', 'IC 2,5%', 'IC 97,5%', 'coefficient standardisé'))| terme | coefficient | IC 2,5% | IC 97,5% | coefficient standardisé |
|---|---|---|---|---|
| constante | 0,001 | 0,001 | 0,001 | -6,893 |
| cr_income | 0,990 | 0,987 | 0,994 | -0,132 |
| cr_per_black | 1,005 | 1,002 | 1,008 | 0,071 |
| cr_per_hispanic | 1,003 | 0,999 | 1,007 | 0,042 |
| cr_per_atleast_hs | 0,988 | 0,977 | 0,999 | -0,074 |
| cr_per_nursing | 1,823 | 1,516 | 2,191 | 0,203 |
| cr_X65plus | 0,998 | 0,986 | 1,010 | -0,008 |
| cr_political_leaning | 1,515 | 1,337 | 1,716 | 0,129 |
| cr_strict_p3 | 0,992 | 0,988 | 0,996 | -0,078 |
| cr_mask_usage_p3 | 0,984 | 0,952 | 1,016 | -0,030 |
| cr_google_p3 | 1,008 | 1,005 | 1,011 | 0,057 |
| cr_dist_to_airport | 0,999 | 0,999 | 1,000 | -0,026 |
| cr_density | 1,000 | 1,000 | 1,000 | 0,000 |
Finalement, nous pouvons extraire les effets aléatoires du modèle et plus spécifiquement nos coefficients variant spatialement. Pour cela, nous devons additionner le coefficient général et sa variation spatiale. Puisque nous avons centré et réduit nos variables, nous devons diviser les coefficients obtenus par l’écart type original de ces variables pour pouvoir les interpréter dans leur échelle originale. Effet, il reste à appliquer la fonction exponentielle pour obtenir l’effet local multiplicatif des variables indépendantes sur le taux de décès. La fonction predict du package sdmTMB permet d’extraire à la fois les valeurs prédites, mais aussi les coefficients spatiaux du modèle.
library(matrixStats)
set.seed(888)
# Extraction des prédictions
preds <- predict(model2, type = 'link')
# Récupération de l'intercepte spatial
data_mode1$rand_intercept <- exp(preds$omega_s)
# Extraction de 999 simulations des valeurs locales des coefficients spatiaux
preds2 <- predict(model2, type = 'link', nsim = 999, sims_var = 'zeta_s')
# Extraction de 999 simulations des valeurs locales de la constante spatiale
preds3 <- predict(model2, type = 'link', nsim = 999, sims_var = 'omega_s')
# Pour chacun des coefficients spatiaux, déterminer si la variation spatiale est
# significativement différente de 0 au seuil 0,05
pvals <- sapply(preds2, function(tab){
qtl <- rowQuantiles(tab, probs = c(0.025, 0.975))
test <- ((qtl[,1] < 0) & (qtl[,2] < 0)) | ((qtl[,1] > 0) & (qtl[,2] > 0))
return(test)
})
pvals <- data.frame(pvals)
# Idem avec l'intercepte spatiale
qtl <- rowQuantiles(preds3, probs = c(0.025, 0.975))
test <- ((qtl[,1] < 0) & (qtl[,2] < 0)) | ((qtl[,1] > 0) & (qtl[,2] > 0))
data_mode1$rand_intercept_sign <- test
# Récupération des coefficients spatiaux pour nos différentes variables
# avec un effet spatial
sp_vars <- c('cr_per_atleast_hs', 'cr_X65plus', 'cr_income', 'cr_per_nursing')
for(var in sp_vars){
# récupération du coefficient fixe de base
base_coeff <- tab_fixe$estimate_std[tab_fixe$term == var]
# récupération des variations spatiales du coefficient
sp_coeff <- preds[[paste0('zeta_s_', var)]]
# addition et conversion vers l'échelle originale des données
loc_coeff <- (base_coeff + sp_coeff) / sd_df$sd[sd_df$var == var]
# application de la fonction exponentielle pour avoir l'effet multiplicatif
# sur le taux de décès
exp_loc_coeff <- exp(loc_coeff)
data_mode1[[paste0('sp_coeff_', var)]] <- exp_loc_coeff
data_mode1[[paste0('sp_sign_', var)]] <- pvals[[var]]
}
legende_parametres <- list(text.separator = "à",
decimal.mark = ",",
big.mark = " ",
digits = 2)
tmap_options(frame = FALSE)
tm_shape(data_mode1) +
tm_polygons(
col = NULL,
fill = 'sp_coeff_cr_per_atleast_hs',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Coef. pour le diplôme d'études secondaires",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(data_mode1, !data_mode1$sp_sign_cr_per_atleast_hs)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)
tm_shape(data_mode1) +
tm_polygons(
col = NULL,
fill = 'sp_coeff_cr_income',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Coef. pour le revenu",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(data_mode1, !data_mode1$sp_sign_cr_income)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)
tm_shape(data_mode1) +
tm_polygons(
col = NULL,
fill = 'sp_coeff_cr_per_nursing',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Coef. pour la population en soin de longue durée",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(data_mode1, !data_mode1$sp_sign_cr_per_nursing)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)
tm_shape(data_mode1) +
tm_polygons(
col = NULL,
fill = 'sp_coeff_cr_X65plus',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Coef. pour les 65 ans et plus",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(data_mode1, !data_mode1$sp_sign_cr_X65plus)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)
tm_shape(data_mode1) +
tm_polygons(
col = NULL,
fill = 'rand_intercept',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 1,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Constante aléatoire spatial",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(data_mode1, !data_mode1$rand_intercept_sign)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)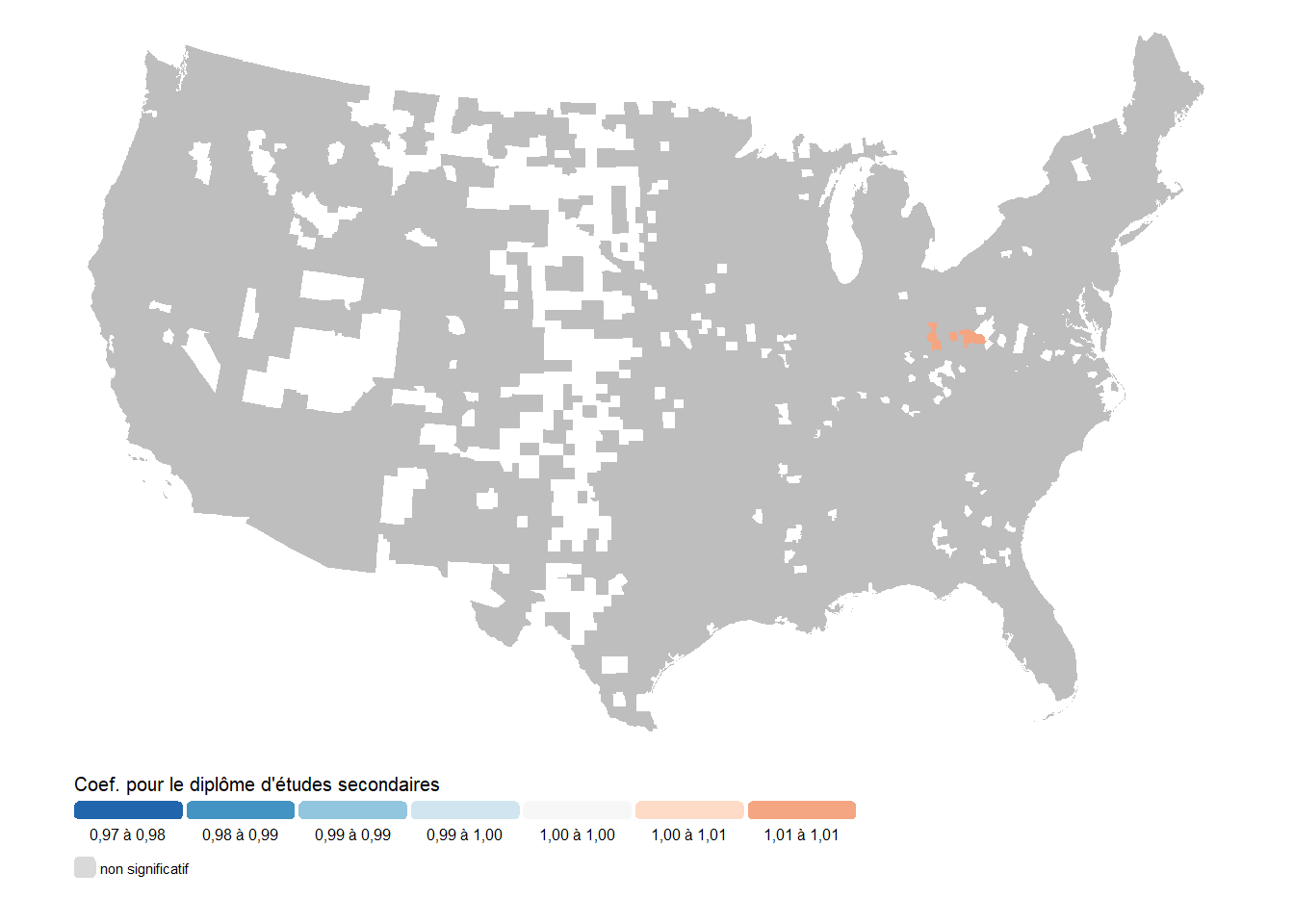
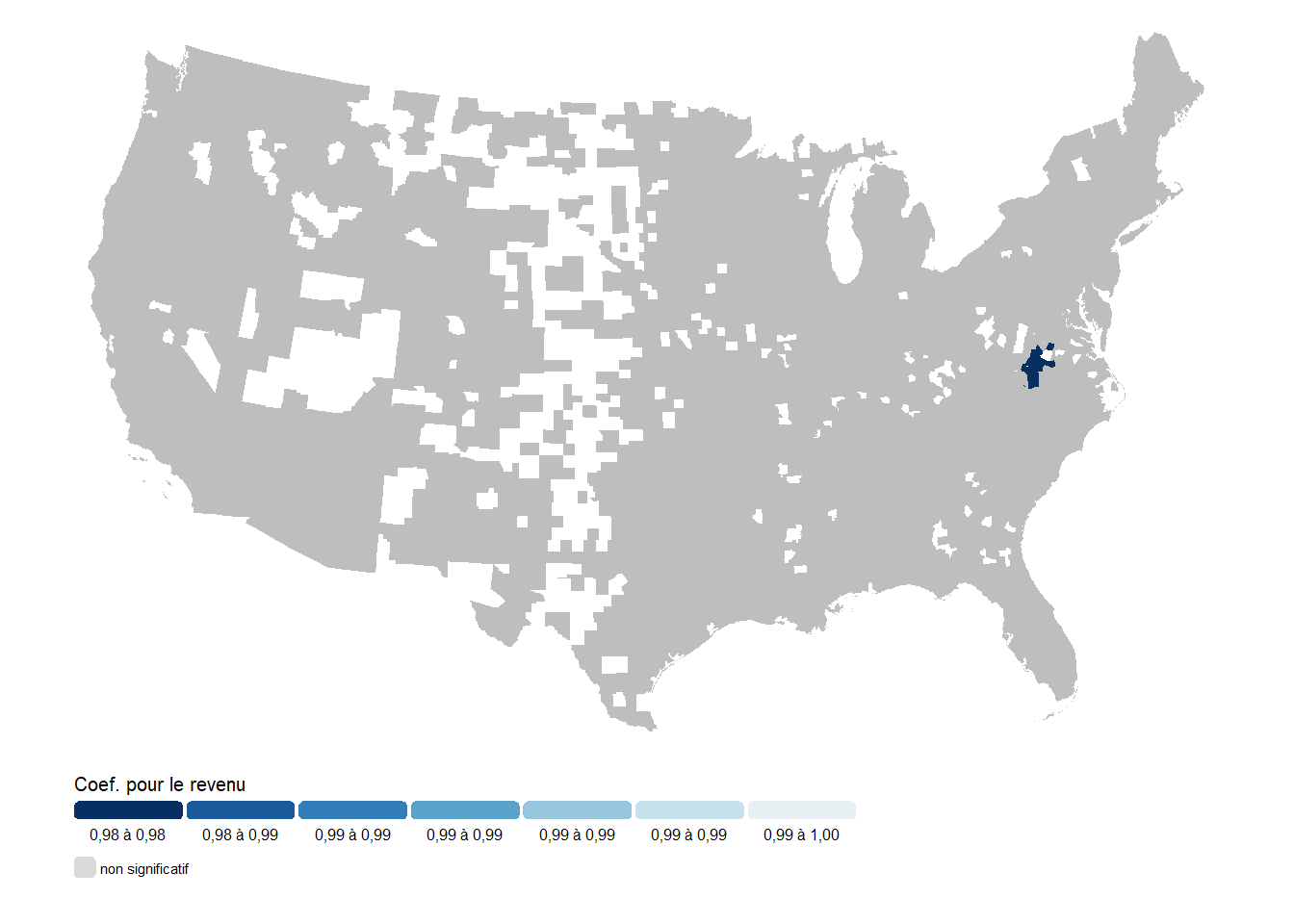
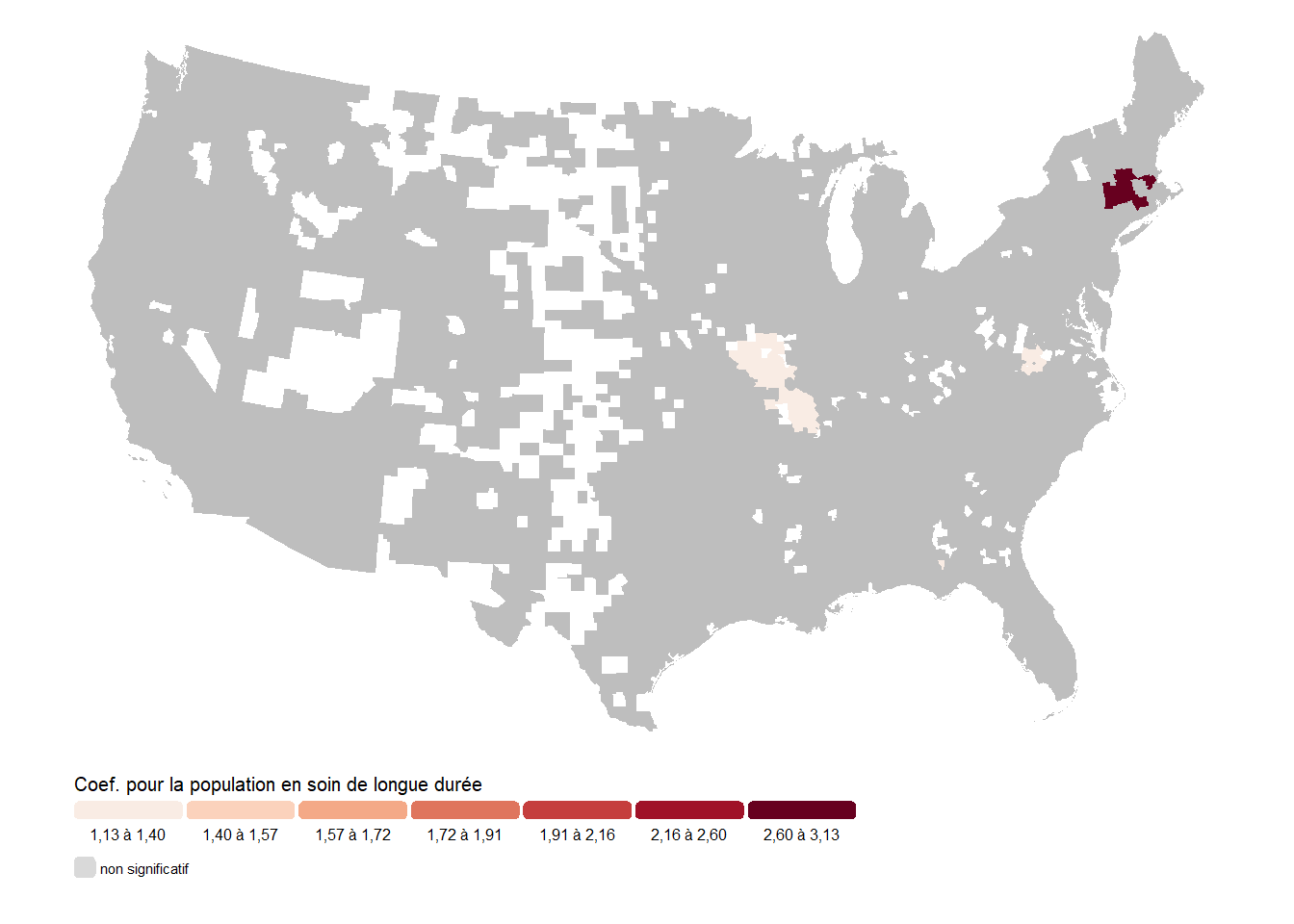
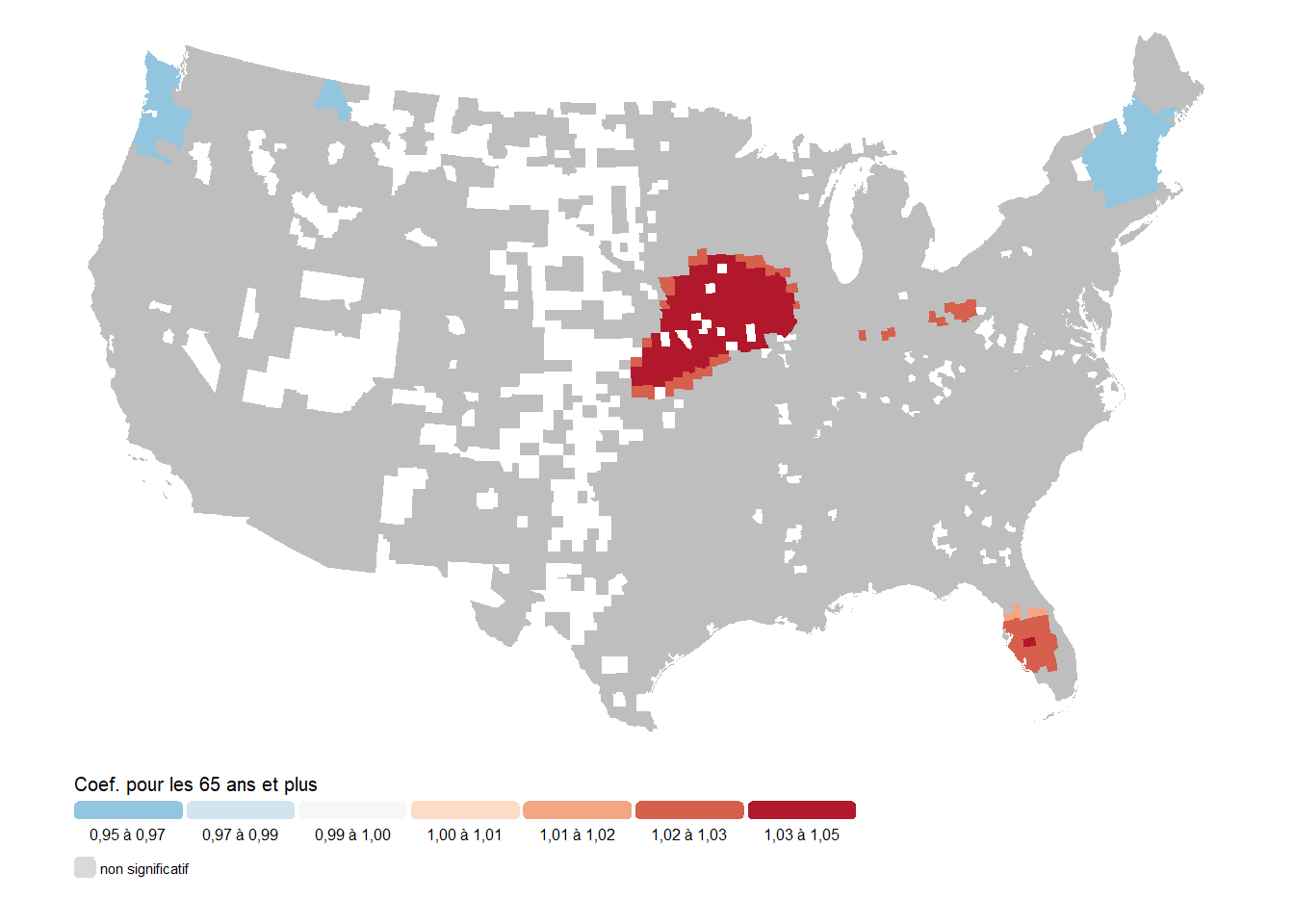
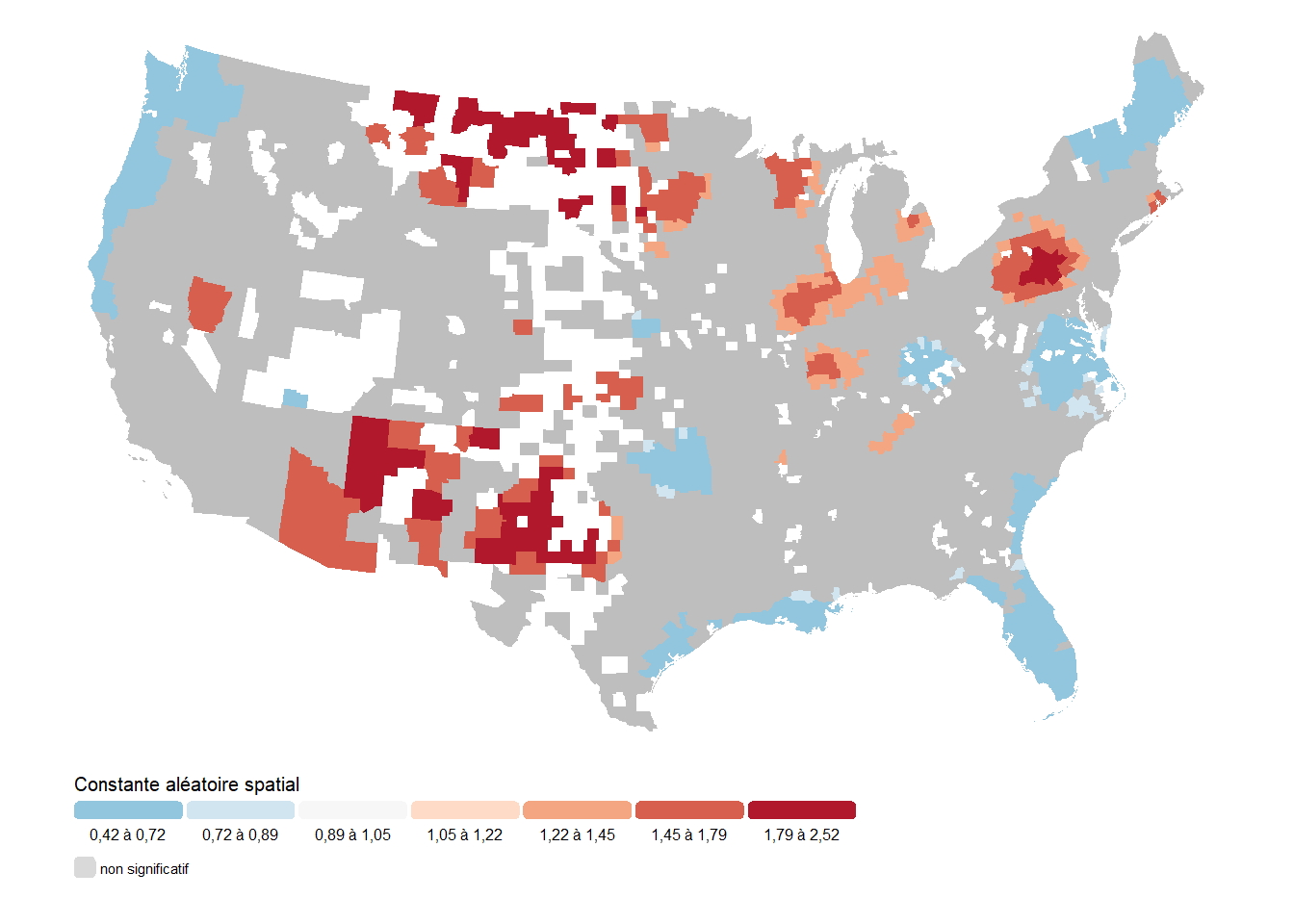
Attention, dans les cartes ci-dessus (figures 10.16 à 10.20), les comtés grisés correspondent à des comtés pour lesquels le coefficient cartographié n’a pas significativement varié spatialement. Dans ces cas-ci, l’effet qui s’applique dans le comté est tout simplement l’effet fixe général pour ce coefficient.
Premièrement, nous remarquons que les variations spatiales des coefficients du niveau d’éducation et du revenu sont toutes les deux beaucoup trop faibles pour avoir un impact réellement significatif. Il serait donc plus prudent de considérer que ces deux coefficients ne varient pas spatialement.
Deuxièmement, pour le coefficient associé à la population en soin de longue durée, trois zones semblent caractérisées par des variations locales supérieures à zéro, soit une partie de l’État du Missouri, le nord de la Virginie en frontière avec l’État de Washington, et enfin quelques Comtés de l’État de New York. Cet effet suggère que la mortalité associée à cette population a été plus importante dans ces zones. Avec des coefficients variant entre 1,13 et 1,40 dans les deux premières zones et entre 2,5 et plus de 3 pour la troisième.
Troisièmement, le pourcentage de la population de 65 ans et plus a un effet variant un peu plus spatialement avec deux zones dans lesquels elle est associée avec une réduction du taux de décès (États de New York, New Hampshire, Vermont, Massachusetts, Connecticut et Rhode Island, et l’ouest des États de Washington et de l’Oregon); et trois zones dans lesquelles elle est associée avec une augmentation du taux de décès (États de l’Iowa, Nebraska, Kansas, Ohio et Floride).
Finalement, la constante spatiale montre un impact significatif dans un plus grand nombre de Comtés. L’ouest des États-Unis tend à avoir des taux de décès plus élevés (jusqu’à 2,5 fois) toutes choses étant égales par ailleurs. À l’inverse, le nord-ouest avec les États de Washington, de l’Idaho, de l’Oregon et le nord de la Californie sont caractérisés par des taux plus faibles (jusqu’à 50 %). Dans l’est, l’État de New York et la Pennsylvanie sont aussi caractérisés par des taux plus élevés, alors que la Virginie et la Caroline du Nord ont tendance à avoir des taux plus faibles.
10.3 Quiz de révision
10.4 Exercices de révision
Exercice 1. Réalisation d’un modèle GAM avec des splines et coefficients variant spatialement
Complétez le code ci-dessous.
library(sf, quietly = TRUE)
library(ggplot2, quietly = TRUE)
library(tmap, quietly = TRUE)
library(dplyr, quietly = TRUE)
library(ggpubr, quietly = TRUE)
library(mgcv, quietly = TRUE)
library(spdep, quietly = TRUE)
library(collapse, quietly = TRUE)
library(gratia, quietly = TRUE)
load("data/Lyon.Rdata")
xy <- st_coordinates(st_centroid(LyonIris))
LyonIris$X <- xy[,1]
LyonIris$Y <- xy[,2]
# Modèle non spatial avec une distribution gaussienne
model1 <- gam(NO2 ~
Pct0_14 + Pct_65 + Pct_Img + Pct_brevet + NivVieMed,
data = LyonIris, method = 'REML',
family = gaussian(link = "identity"))
summary(model1)
# Modèle intégrant uniquement une constante variant spatialement
model2 <- gam(NO2 ~
Pct0_14 + Pct_65 + Pct_Img + Pct_brevet + NivVieMed +
à compléter, # Spline pour la constante
data = LyonIris, method = 'REML',
family = gaussian(link = "identity"))
summary(model2)
# Modèle intégrant intégrant les coefficients variant spatialement
model3 <- gam(NO2 ~
# à compléter Splines pour les variables indépendantes
data = LyonIris, method = 'REML',
family = gaussian(link = "identity"))
summary(model3)
round(concurvity(model3),3)
# Modèle intégrant intégrant avec uniquement le niveau de vie variant spatialement
model3 <- gam(à compléter)
summary(model3)
comp_df <- AIC(model1, model2, model3)
comp_df$REML <- c(model1$gcv.ubre, model2$gcv.ubre, model3$gcv.ubre)
comp_df$R2 <- c(summary(model1)$r.sq,
summary(model2)$r.sq,
summary(model3)$r.sq)
knitr::kable(comp_df, row.names = TRUE, digits = 2)
LyonIris$residual_1 <- residuals(model1, type = 'scaled.pearson')
LyonIris$residual_2 <- residuals(model2, type = 'scaled.pearson')
LyonIris$residual_3 <- residuals(model3, type = 'scaled.pearson')
knn_list <- knearneigh(st_centroid(LyonIris), k = 10)
nb_list <- knn2nb(knn_list, sym = TRUE)
listw <- nb2listwdist(nb_list, st_centroid(LyonIris), style = 'W', type = 'idw', alpha = 2)
test1 <- moran.mc(LyonIris$residual_1, listw = listw, nsim = 999)
test2 <- moran.mc(LyonIris$residual_2, listw = listw, nsim = 999)
test3 <- moran.mc(LyonIris$residual_3, listw = listw, nsim = 999)
tableau <- data.frame(
variable = c('residus1', 'residus2', 'residus3'),
I = c(test1$statistic, test2$statistic, test3$statistic),
P = c(test1$p.value, test2$p.value, test3$p.value)
)
print(tableau)
summary(model3)
# Cartographie des effets spatiaux
library(terra)
library(gratia)
library(matrixStats)
mask_data <- LyonIris %>%
st_union() %>%
vect()
# Préparation d'un ensemble de points de prédictions formant une grille
# régulière de quadrats de 200 mètres de coté
bbox <- st_bbox(mask_data)
coords <- expand.grid(
X = seq(bbox$xmin, bbox$xmax, 100),
Y = seq(bbox$ymin, bbox$ymax, 100)
)
# Création du dataframe pour les prédictions
pred_df <- coords
pred_df$Pct0_14 <- 0
pred_df$Pct_brevet <- 0
pred_df$Pct_65 <- 0
pred_df$NivVieMed <- mean(LyonIris$NivVieMed)
# Prédictions à partir du modèle
preds <- predict(à compléter)
preds <- data.frame(preds)
preds <- cbind(pred_df[, c("X", "Y")], preds)
names(preds) <- c("X", "Y", "Pct0_14", "Pct_brevet", "Pct_65", "spline_NivVieMed")
# Conversion des prédictions en objets raster pour la cartographie
vars <- c("X", "Y","spline_NivVieMed")
data_rast <- as.matrix(preds[, vars])
raster_NivVieMed <- rast(data_rast[,c(1,2,3)],type = 'xyz')
crs(raster_NivVieMed) <- crs(LyonIris)
# Cartographie de l'effet spatial de niveau de vie
legende_parametres <- list(text.separator = "à",
decimal.mark = ",",
big.mark = " "
)
tmap_options(frame = FALSE)
tm_shape(mask(raster_NivVieMed, mask_data)) +
tm_raster(
col.scale = tm_scale_intervals(
n = 6,
midpoint = 0,
style = "pretty",
values = '-brewer.rd_bu',
label.format = legende_parametres),
col.legend = tm_legend(title = "Niveau de vie",
position = tm_pos_out(pos.h = "left", pos.v = "top"),
frame = FALSE
)
)Correction à la section 11.10.1.
Exercice 2. Réalisation de mesh pour des modèles GLMM
Complétez le code ci-dessous.
load("data/Lyon.Rdata")
library(sf, quietly = TRUE)
library(ggplot2, quietly = TRUE)
library(tmap, quietly = TRUE)
library(dplyr, quietly = TRUE)
library(spdep, quietly = TRUE)
library(DHARMa, quietly = TRUE)
library(sdmTMB, quietly = TRUE)
# Récupération en mise à l'échelle des coordonnées spatiales (division par 100)
vars <- c('Pct0_14', 'Pct_65', 'Pct_Img', 'Pct_brevet', 'NivVieMed')
XY <- st_coordinates(st_centroid(LyonIris))
LyonIris <- LyonIris[, c("NO2", vars)]
LyonIris$X <- XY[,1] / 100
LyonIris$Y <- XY[,2] / 100
# Standardisation des différentes variables quantitatives
for(var in vars){
à compléter
}
# Réalisation de la mesh avec des valeurs de 20, 1 et 5
mesh1 <- à compléter
mesh2 <- à compléter
mesh3 <- à compléter
plot(mesh1)
plot(mesh2)
plot(mesh3)Correction à la section 11.10.2.
Exercice 3. Réalisation d’un modèle GLMM spatial avec le package sdmTMB
Complétez le code ci-dessous.
# Modèle MCO
modele_mco <- lm(formule, data = LyonIris)
# Premier modèle avec uniquement la constante variant spatialement
model1 <- sdmTMB(
à compléter
)
# Analyse des résidus simulés du modèle
simulations <- simulate(model1, nsim = 500, type = "mle-mvn")
resids <- dharma_residuals(simulations, model1, return_DHARMa = TRUE)
plot(resids)
# Second modèle qui fait aussi varier spatialement les variables indépendantes
model2 <- sdmTMB(
à compléter
)
# Identification des variables qui varient spatialement
tidy(model2, effects = 'ran_pars', conf.int = TRUE) %>%
knitr::kable(digits = 3)
# Troisième modèle avec uniquement les variables à faire
# varier spatialement
model3 <- sdmTMB(
data = st_drop_geometry(LyonIris),
formula = NO2 ~
cr_Pct0_14 + cr_Pct_65 + cr_Pct_Img + cr_Pct_brevet + cr_NivVieMed,
mesh = mesh2,
spatial = TRUE,
spatial_varying = ~ 1 + cr_Pct_Img + cr_NivVieMed,
family = gaussian(link = "identity"),
)
# analyse des résidus simulés du modèle
simulations <- simulate(model3, nsim = 500, type = "mle-mvn")
resids <- dharma_residuals(simulations, model3, return_DHARMa = TRUE)
plot(resids)
caic1 <- cAIC(model1)
caic2 <- cAIC(model2)
caic3 <- cAIC(model3)
print(c(caic1, caic2, caic3))
# Extraction des coefficients et de leurs intervalles de confiance
tab_fixe <- tidy(model3, effects = 'fixed', conf.int = TRUE)
# Récupération des écarts types
vars <- c('Pct0_14', 'Pct_65', 'Pct_Img', 'Pct_brevet', 'NivVieMed')
sd_values <- sapply(vars, function(x){
sd(LyonIris[[x]])
})
sd_df <- data.frame(
sd = c(1,sd_values),
var = c('(Intercept)', paste0('cr_',vars))
)
# Application des écarts types aux effets estimés
ids <- match(tab_fixe$term, sd_df$var)
tab_fixe$estimate_std <- tab_fixe$estimate
print(tab_fixe)
for(col in c("estimate", "conf.low", "conf.high")){
tab_fixe[[col]] <- tab_fixe[[col]] / sd_df$sd[ids]
}
tab_fixe$std.error <- NULL
# Extraction des prédictions
preds <- predict(model3, type = 'link')
# Récupération de la constante spatiale
LyonIris$rand_intercept <- preds$omega_s
# Extraction de 999 simulations des valeurs locales des coefficients spatiaux
library(matrixStats)
set.seed(888)
preds2 <- predict(model3, type = 'link', nsim = 999, sims_var = 'zeta_s')
# Extraction de 999 simulations des valeurs locales de la constante spatiale
preds3 <- predict(model3, type = 'link', nsim = 999, sims_var = 'omega_s')
# Pour chacun des coefficients spatiaux, déterminer si la variation spatiale est
# significativement différente de 0 au seuil 0.05
pvals <- sapply(preds2, function(tab){
qtl <- rowQuantiles(tab, probs = c(0.025, 0.975))
test <- ((qtl[,1] < 0) & (qtl[,2] < 0)) | ((qtl[,1] > 0) & (qtl[,2] > 0))
return(test)
})
pvals <- data.frame(pvals)
# idem avec la constante spatiale
qtl <- rowQuantiles(preds3, probs = c(0.025, 0.975))
test <- ((qtl[,1] < 0) & (qtl[,2] < 0)) | ((qtl[,1] > 0) & (qtl[,2] > 0))
LyonIris$rand_intercept_sign <- test
table(LyonIris$rand_intercept_sign)
# Récupération des coefficients spatiaux pour nos différentes variables
# avec un effet spatial
sp_vars <- c('cr_Pct_Img', 'cr_NivVieMed')
for(var in sp_vars){
# récupération du coefficient fixe de base
base_coeff <- tab_fixe$estimate_std[tab_fixe$term == var]
# récupération des variations spatiales du coefficient
sp_coeff <- preds[[paste0('zeta_s_', var)]]
# addition et conversion vers l'échelle originale des données
loc_coeff <- (base_coeff + sp_coeff) / sd_df$sd[sd_df$var == var]
LyonIris[[paste0('sp_coeff_', var)]] <- loc_coeff
LyonIris[[paste0('sp_sign_', var)]] <- pvals[[var]]
}
table(LyonIris$sp_sign_cr_Pct_Img)
table(LyonIris$sp_sign_cr_NivVieMed)
legende_parametres <- list(text.separator = "à",
decimal.mark = ",",
big.mark = " ",
digits = 2)
tmap_options(frame = FALSE)
tm_shape(LyonIris) +
tm_polygons(
col = NULL,
fill = 'rand_intercept',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 0,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Constante aléatoire spatial",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(LyonIris, !LyonIris$rand_intercept_sign)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)
tm_shape(LyonIris) +
tm_polygons(
col = NULL,
fill = 'sp_coeff_cr_Pct_Img',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 0,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Constante aléatoire spatial",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(LyonIris, !LyonIris$sp_sign_cr_Pct_Img)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)
tm_shape(LyonIris) +
tm_polygons(
col = NULL,
fill = 'sp_coeff_cr_NivVieMed',
fill.scale = tm_scale_intervals(
style = 'fisher', n = 7, midpoint = 0,
values = '-brewer.rd_bu',
label.format = legende_parametres),
fill.legend = tm_legend(
title = "Constante aléatoire spatial",
position = tm_pos_out("center", "bottom"),
frame = FALSE,
orientation = "landscape")
) +
tm_shape(subset(LyonIris, !LyonIris$sp_sign_cr_NivVieMed)) +
tm_polygons(col = NULL, fill = 'grey') +
tm_add_legend(type = 'polygons',
position = tm_pos_out("center", "bottom"),
labels = 'non significatif',
col = NA)Correction à la section 11.10.3.